Câu hỏi
Cho lăng trụ tam giác đều có cạnh đáy bằng \(a\), cạnh bên bằng \(b\). Thể tích của khối cầu đi qua các đỉnh của lăng trụ bằng
- A \(\frac{1}{{18\sqrt 3 }}\sqrt {{{\left( {4{a^2} + 3{b^2}} \right)}^3}} \)
- B \(\frac{\pi }{{18\sqrt 3 }}\sqrt {{{\left( {4{a^2} + 3{b^2}} \right)}^3}} \)
- C \(\frac{\pi }{{18\sqrt 3 }}\sqrt {{{\left( {4{a^2} + {b^2}} \right)}^3}} \)
- D \(\frac{\pi }{{18\sqrt 2 }}\sqrt {{{\left( {4{a^2} + 3{b^2}} \right)}^3}} \)
Phương pháp giải:
- Xác định tâm mặt cầu ngoại tiếp lăng trụ (trung điểm đoạn nối tâm).
- Tính bán kính theo Pitago suy ra thể tích \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết:
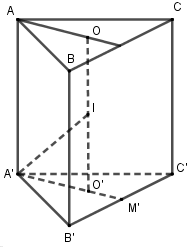
Gọi \(O,O'\) lần lượt là tâm đáy, \(I\) là trung điểm của \(OO'\) thì \(I\) là tâm mặt cầu ngoại tiếp lăng trụ và bán kính \(R = IA'\).
Ta có: \(A'O' = \frac{2}{3}A'M' = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3};\,\,IO' = \frac{1}{2}OO' = \frac{b}{2}\)
Do đó \(IA' = \sqrt {IO{'^2} + A'O{'^2}} = \sqrt {\frac{{{b^2}}}{4} + \frac{{{a^2}}}{3}} = \sqrt {\frac{{4{a^2} + 3{b^2}}}{{12}}} \).
Thể tích khối cầu \(V = \frac{4}{3}\pi IA{'^2} = \frac{4}{3}\pi .{\left( {\sqrt {\frac{{4{a^2} + 3{b^2}}}{{12}}} } \right)^3}\) \( = \frac{{4\pi }}{{3.12\sqrt {12} }}\sqrt {{{\left( {4{a^2} + 3{b^2}} \right)}^3}} = \frac{\pi }{{18\sqrt 3 }}\sqrt {{{\left( {4{a^2} + 3{b^2}} \right)}^3}} \)
Chọn B.