Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, cạnh bên \(SA = a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Trên \(SB,SD\) lần lượt lấy hai điểm \(M,N\) sao cho \(\dfrac{{SM}}{{SB}} = m > 0,\,\,\dfrac{{SN}}{{SD}} = n > 0\). Tính thể tích lớn nhất \({V_{\max }}\) của khối chóp \(S.AMN\) biết \(2{m^2} + 3{n^2} = 1\).
- A \({V_{\max }} = \dfrac{{{a^3}\sqrt 6 }}{{72}}\).
- B \({V_{\max }} = \dfrac{{{a^3}}}{{48}}\).
- C \({V_{\max }} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\).
- D
\({V_{\max }} = \dfrac{{{a^3}}}{6}\).
Phương pháp giải:
Lập tỉ lệ thể tích của khối chóp \(S.AMN\) và khối chóp \(S.ABCD\).
Sử dụng BĐT để biện luận GTLN của thể tích khối chóp \(S.AMN\).
Lời giải chi tiết:
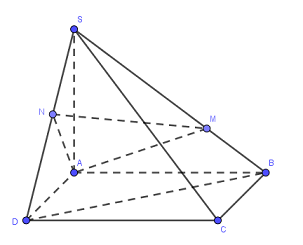
Thể tích khối chóp \(S.ABCD\) là: \({V_{S.ABCD}} = \dfrac{1}{3}.a.{a^2} = \dfrac{1}{3}{a^3}\)
Ta có: \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}} = mn \Rightarrow {V_{S.AMN}} = mn{V_{S.ABD}} = \dfrac{1}{2}mn{V_{S.ABCD}}\)
Mà : \(1 = 2{m^2} + 3{n^2} \ge 2\sqrt {2{m^2}.3{n^2}} \Rightarrow 1 \ge 2\sqrt 6 .mn \Rightarrow mn \le \dfrac{{\sqrt 6 }}{{12}}\)
\( \Rightarrow {V_{S.AMN}} = \dfrac{1}{2}mn{V_{S.ABCD}} \le \dfrac{1}{2}.\dfrac{{\sqrt 6 }}{{12}}.{V_{S.ABCD}} = \dfrac{1}{2}.\dfrac{{\sqrt 6 }}{{12}}.\dfrac{{{a^3}}}{3} = \dfrac{{{a^3}\sqrt 6 }}{{72}}\)
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}2{m^2} + 3{n^2} = 1\\2{m^2} = 3{n^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = \dfrac{1}{4}\\{n^2} = \dfrac{1}{6}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{1}{2}\\n = \dfrac{1}{{\sqrt 6 }}\end{array} \right.\)
Vậy, thể tích lớn nhất của khối chóp \(S.AMN\)là \({V_{\max }}\)\( = \dfrac{{{a^3}\sqrt 6 }}{{72}}\).
Chọn: A







