Câu hỏi
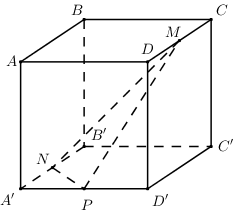
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm các cạnh \(CD,\,\,A'B',\,\,A'D'\). Thể tích khối tứ diện \(A'MNP\) bằng:
- A \(\frac{{{a^3}}}{{16}}\)
- B \(\frac{{{a^3}}}{{32}}\)
- C \(\frac{{{a^3}}}{{12}}\)
- D \(\frac{{{a^3}}}{{24}}\)
Phương pháp giải:
Sử dụng công thức \({V_{chop}} = \frac{1}{3}{S_{day}}.h\).
Lời giải chi tiết:
Ta có \({V_{A'MNP}} = \frac{1}{3}d\left( {M;\left( {A'B'C'D'} \right)} \right).{S_{A'NP}} = \frac{1}{3}.a.\frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^3}}}{{24}}\).
Chọn D.
Câu hỏi trước
