Câu hỏi
Một sóng ngang hình sin truyền theo phương ngang dọc theo một sợi dây đàn hồi rất dài có biên độ không đổi và có bước sóng lớn hơn 30 cm. Trên dây có hai điểm A và B cách nhau 15 cm (A gần nguồn hơn so với B). Chọn trục Ox thẳng đứng chiều dương hướng lên, gốc tọa độ O tại vị trí cân bằng của nguồn. M và N tương ứng là hình chiếu của A và B lên trục Ox. Phương trình dao động của N có dạng \({x_N} = acos(\omega t + \frac{\pi }{6})cm\) ; khi đó vận tốc tương đối của N đối với M biến thiên theo thời gian với phương trình \({v_{NM}} = bcos(20\pi t{\rm{ }} + \frac{\pi }{2}){\rm{ }}cm/s\) . Biết a, ω và b là các hằng số dương. Tốc độ truyền sóng trên dây là
- A 350 cm/s
- B 200 cm/s
- C 450 cm/s
- D 500 cm/s
Phương pháp giải:
Phương pháp : Áp dụng giản đồ vecto trong sóng cơ học
Lời giải chi tiết:
Cách giải :
Từ biểu thức vận tốc ta có tần số truyền sóng trên dây là \(f = 10Hz\)
Vận tốc tương đối của N đối với N là \({v_{MN}} = b\cos \left( {20\pi t + \frac{\pi }{2}} \right) = > {x_{MN}} = \frac{b}{{20\pi }}\sin \left( {20\pi t + \frac{\pi }{2}} \right) = \frac{b}{{20\pi }}\cos \left( {20\pi t} \right)cm = {x_N} - {x_M}\)
Kết hợp với phường trình sóng tại N và biểu diễn trên giản đồ vecto ta được
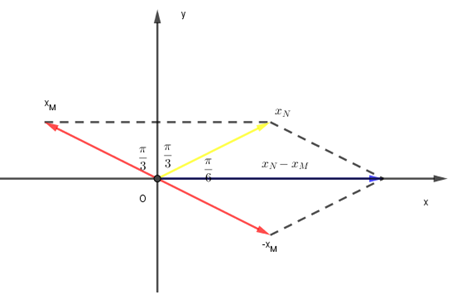
Độ lệch pha giữa N và M là \({\varphi _{NM}} = \frac{{2\pi }}{3} = > \frac{{2\pi }}{3} = \frac{{2\pi d}}{\lambda } = > \lambda = 3d = 3.15 = 45cm\)
Vận tốc truyền sóng trên dây là \(v = \lambda f = 45.10 = 450cm/s\)
Chọn C







