Phương pháp giải:

Sử dụng phương trình đường tròn để tìm giá trị lớn nhất của \(Q\) từ đó tìm \(x,y.\)

Lời giải chi tiết:

Ta có \(Q = \sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 3} \right)}^2}}  + \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} \)

\(\begin{array}{l} \Rightarrow {Q^2} = {\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + 2\sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 3} \right)}^2}} .\sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} \\ \le 2\left[ {{{\left( {x + 1} \right)}^2} + {{\left( {y - 3} \right)}^2} + {{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} \right] = 4\left( {{x^2} + {y^2} - 2y + 6} \right) = 4\left[ {{x^2} + {{\left( {y - 1} \right)}^2}} \right] + 20.\end{array}\) 

Vì Q đạt giá trị lớn nhất nên \({Q^2}\) đạt giá trị lớn nhất \( \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2}\) đạt giá trị lớn nhất

Ta có x, y là hai số thực thỏa mãn \({\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 5\)

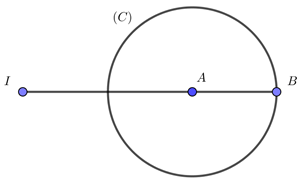
\( \Rightarrow \) \(\left( {x;y} \right)\) là tọa độ điểm thuộc đường tròn \(\left( C \right)\) tâm \(A\left( {4;3} \right)\) bán kính \(R = \sqrt 5 \)

Mặt khác để \({x^2} + {\left( {y - 1} \right)^2}\) đạt giá trị lớn nhất  \( \Leftrightarrow \left( {x;\,y} \right)\) cũng là điểm thuộc đường tròn \(\left( {C'} \right)\) tâm \(I\left( {0;1} \right)\) sao cho bán kính lớn nhất.

Gọi \(\left( C \right)\) giao tia đối của tia AI tại B

Ta có: \(IA = \sqrt {{4^2} + {2^2}}  = \sqrt {20}  = 2\sqrt 5  > R\)

\( \Rightarrow \) I nằm ngoài đường tròn \(\left( C \right)\)

\( \Rightarrow \) Để thỏa mãn đề bài \( \Leftrightarrow B\left( {x;y} \right)\)

\(\overrightarrow {IA}  = \left( {4;2} \right) \Rightarrow \overrightarrow n  = \left( { - 2;4} \right)\)

Phương trình IA: \( - 2x + 4\left( {y - 1} \right) = 0 \Leftrightarrow  - x + 2y - 2 = 0\)

\(\begin{array}{l}\left\{ \begin{array}{l}B \in \left( {IA} \right)\\B \in \left( C \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l} - x + 2y - 2 = 0\\{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\{\left( {2y - 6} \right)^2} + {\left( {y - 3} \right)^2} = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\5{\left( {y - 3} \right)^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\\left[ \begin{array}{l}y - 3 = 1\\y - 3 =  - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\\left[ \begin{array}{l}y = 4\\y = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 6\\y = 4\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}B\left( {6;4} \right)\\B\left( {2;2} \right)\end{array} \right.\end{array}\)

Vì B và I khác phía với A \( \Rightarrow B\left( {6;4} \right)\)

\( \Rightarrow P = x + y = 6 + 4 = 10\)

Chọn B.