Phương pháp giải:

Biến đổi phương trình đã cho, đưa phương trình về dạng \(f(x)=g(x; \,m)\)

Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số \(y=f(x)\) và đường thẳng \(y=g(x; \, m).\)

Chứng minh đường thẳng \(y=g(x; \, \, m)\) luôn đi qua 1 điểm cố định.

Dựa vào đồ thị hàm số để đưa ra kết luận đúng.

Lời giải chi tiết:

Ta có: \({x^3} - 3{x^2} - mx + m + 2 = 0 \Leftrightarrow {x^3} - 3{x^2} + 2 = m\left( {x - 1} \right)\)

Số nghiệm của pt đã cho là số giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) và đường thẳng \(y = m\left( {x - 1} \right)\).

Ta thấy đường thẳng \(y = m\left( {x - 1} \right)\) luôn đi qua điểm B(1;0) và có hệ số góc m.

Ta có đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) và họ các đường thẳng \(y = m\left( {x - 1} \right)\):

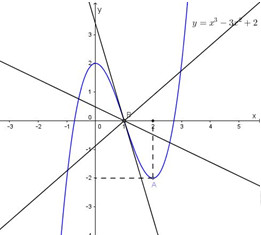
Quan sát đồ thị ta thấy đường thẳng \(y = m\left( {x - 1} \right)\) chỉ có thể cắt đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) tại 1 điểm hoặc tại 3 điểm phân biệt.

Chọn C.