Phương pháp giải:

Phương trình đã cho có dạng: \(|u(x)|.v(x) = m\)

Vẽ đồ thị hàm số \(y=| u(x)|.v(x) \)

Số nghiệm của phương trình \(| u(x)|.v(x) = m\) là số giao điểm của đường thẳng \(y=m\) với đồ thị hàm số \(y=| u(x)|.v(x) .\)

Dựa vào đồ thị hàm số suy ra kết luận đúng.

Lời giải chi tiết:

Áp dụng cách vẽ đồ thị hàm số ở Dạng 7 để vẽ đồ thị hàm số và làm bài toán này.

Số nghiệm của pt \(\left( {{x^2} - 5} \right)\left| {{x^2} - 1} \right| = m\) là số giao điểm của đồ thị hàm số \(y = \left( {{x^2} - 5} \right)\left| {{x^2} - 1} \right|\) và đường thẳng\(y = m\).

Ta có đồ thị hàm số \(y = \left( {{x^2} - 5} \right)\left| {{x^2} - 1} \right|\) như sau:

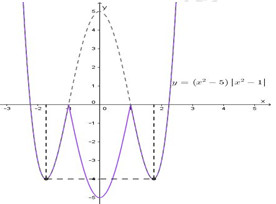
Pt đã cho có 6 nghiệm phân biệt \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \left( {{x^2} - 5} \right)\left| {{x^2} - 1} \right|\) tại 6 điểm phân biệt \( \Leftrightarrow  - 4 < m < 0\).

Chọn B.