Câu hỏi
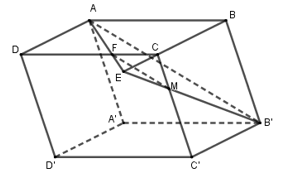
Cho khối hộp\(ABCD.A'B'C'D'\) , điểm \(M\) nằm trên cạnh \(CC'\) thỏa mãn\(CC' = 3CM\). Mặt phẳng \(\left( {A{B^\prime }M} \right)\) chia khối hộp thành hai khối đa diện. Gọi \({V_1}\) là thể tích khối đa diện chứa đỉnh \({A^\prime },{V_2}\) là thể tích khối đa diện chứa đỉnh \(B.\) Tính tỉ số thể tích \({V_1}\) và \({V_2}.\)
- A \(\dfrac{{20}}{7}.\)
- B \(\dfrac{{27}}{7}.\)
- C \(\dfrac{7}{{20}}.\)
- D \(\dfrac{9}{4}.\)
- E \(\dfrac{41}{13}.\)
Phương pháp giải:
- Dựng thiết diện cắt bởi \(\left( {AB'M} \right)\) với hình hộp.
- Sử dụng phương pháp cộng trừ thể tích khối đa diện suy ra các tỉ số thể tích.
Lời giải chi tiết:
Dựng thiết diện của mặt phẳng \(\left( {AB'M} \right)\) với hình hộp như hình vẽ.
Ta có : \(CM//BB' \Rightarrow \dfrac{{EC}}{{B'C'}} = \dfrac{{EM}}{{MB'}} = \dfrac{{CM}}{{MC'}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{EC}}{{EB}} = \dfrac{{EM}}{{EB'}} = \dfrac{{EF}}{{EA}} = \dfrac{1}{3}\).
Đặt thể tích \({V_{ABCD.A'B'C'D'}} = V = {S_{ABB'A'}}.d\left( {C,\left( {ABB'A'} \right)} \right)\).
Mà \({V_{E.ABB'}} = \dfrac{1}{3}{S_{ABB'}}.d\left( {E,\left( {ABB'} \right)} \right)\)
\( \Rightarrow \dfrac{{{V_{E.ABB'}}}}{V} = \dfrac{{\dfrac{1}{3}{S_{ABB'}}.d\left( {E,\left( {ABB'A'} \right)} \right)}}{{{S_{ABB'A'}}.d\left( {C,\left( {ABB'A'} \right)} \right)}}\) \( = \dfrac{1}{3}.\dfrac{{{S_{ABB'}}}}{{{S_{ABB'A'}}}}.\dfrac{{d\left( {E,\left( {ABB'A'} \right)} \right)}}{{d\left( {C,\left( {ABB'A'} \right)} \right)}}\) \( = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{{EB}}{{CB}} = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{3}{2} = \dfrac{1}{4}\)
\( \Rightarrow {V_{E.ABB'}} = \dfrac{1}{4}V\).
Lại có \(\dfrac{{{V_{E.FCM}}}}{{{V_{E.ABB'}}}} = \dfrac{{EF}}{{EA}}.\dfrac{{EC}}{{EB}}.\dfrac{{EM}}{{EB'}} = \dfrac{1}{3}.\dfrac{1}{3}.\dfrac{1}{3} = \dfrac{1}{{27}}\) \( \Rightarrow {V_{E.FCM}} = \dfrac{1}{{27}}{V_{E.ABB'}}\)
\( \Rightarrow {V_{FCM.ABB'}} = \dfrac{{26}}{{27}}{V_{E.ABB'}} = \dfrac{{26}}{{27}}.\dfrac{1}{4}V = \dfrac{{13}}{{54}}V\) hay \({V_2} = \dfrac{{13}}{{54}}V \Rightarrow {V_1} = \dfrac{{41}}{{54}} \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{41}}{{13}}\)
Chọn E.