Phương pháp giải:

Sử dụng phương pháp hình học để tìm tập hợp điểm biểu diễn số phức \(z.\)

Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của \(P\) bằng cách biện luận theo vị trí các điểm đặc biệt của tập hợp điểm tìm được.

Lời giải chi tiết:

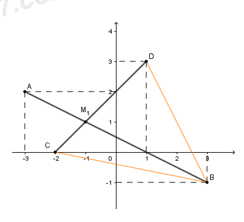
Gọi điểm \(M\left( {x;y} \right)\) là điểm biểu diễn số phức \(z = x + yi\,\left( {x;y \in \mathbb{R}} \right)\)

Điểm \(A\left( { - 3;2} \right)\) biểu diễn số phức \({z_1} = 3 - 2i\)

Điểm \(B\left( {3; - 1} \right)\) biểu diễn số phức \({z_2} =  - 3 + i\)

Khi đó ta có \(AB = \sqrt {{{\left( {3 + 3} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}}  = 3\sqrt 5 \) và

\(\left| {z + 3 - 2i} \right| + \left| {z - 3 + i} \right| = 3\sqrt 5 \) \( \Leftrightarrow \left| {z - {z_1}} \right| + \left| {z - {z_2}} \right| = 3\sqrt 5 \)

\( \Leftrightarrow MA + MB = 3\sqrt 5 \)

Suy ra \(MA + MB = AB \Rightarrow \) tập hợp điểm \(M\) là đường thẳng \(AB.\)

+ Xét \(P = \left| {z + 2} \right| + \left| {z - 1 - 3i} \right|\)

Gọi \(C\left( { - 2;0} \right)\) và \(D\left( {1;3} \right)\) khi đó \(P = \left| {z + 2} \right| + \left| {z - 1 - 3i} \right| = MC + MD\)

Ta tìm \({M_1} \in AB\) sao cho \(MC + MD\) nhỏ nhất và tìm \({M_2} \in AB\) sao cho \(MC + MD\) lớn nhất

Gọi \({M_1}\) là giao của \(AB;CD\) ta thấy \({M_1}C + {M_1}D = CD \le MC + MD \le BC + BD\)

 Giá trị nhỏ nhất của \(P\) là \(m = {M_1}C + {M_1}D = CD = \sqrt {{3^2} + {3^2}}  = 3\sqrt 2 \)

Giá trị lớn nhất của \(P\) là \(M = BC + BD = \sqrt {{5^2} + {{\left( { - 1} \right)}^2}}  + \sqrt {{2^2} + {{\left( { - 4} \right)}^2}}  = \sqrt {26}  + 2\sqrt 5 \)

Chọn C.