Phương pháp giải:

Giao thoa sóng, định lí hàm số sin, bất đẳng thức Bu-nhi-a-cốp-xki. 

Lời giải chi tiết:

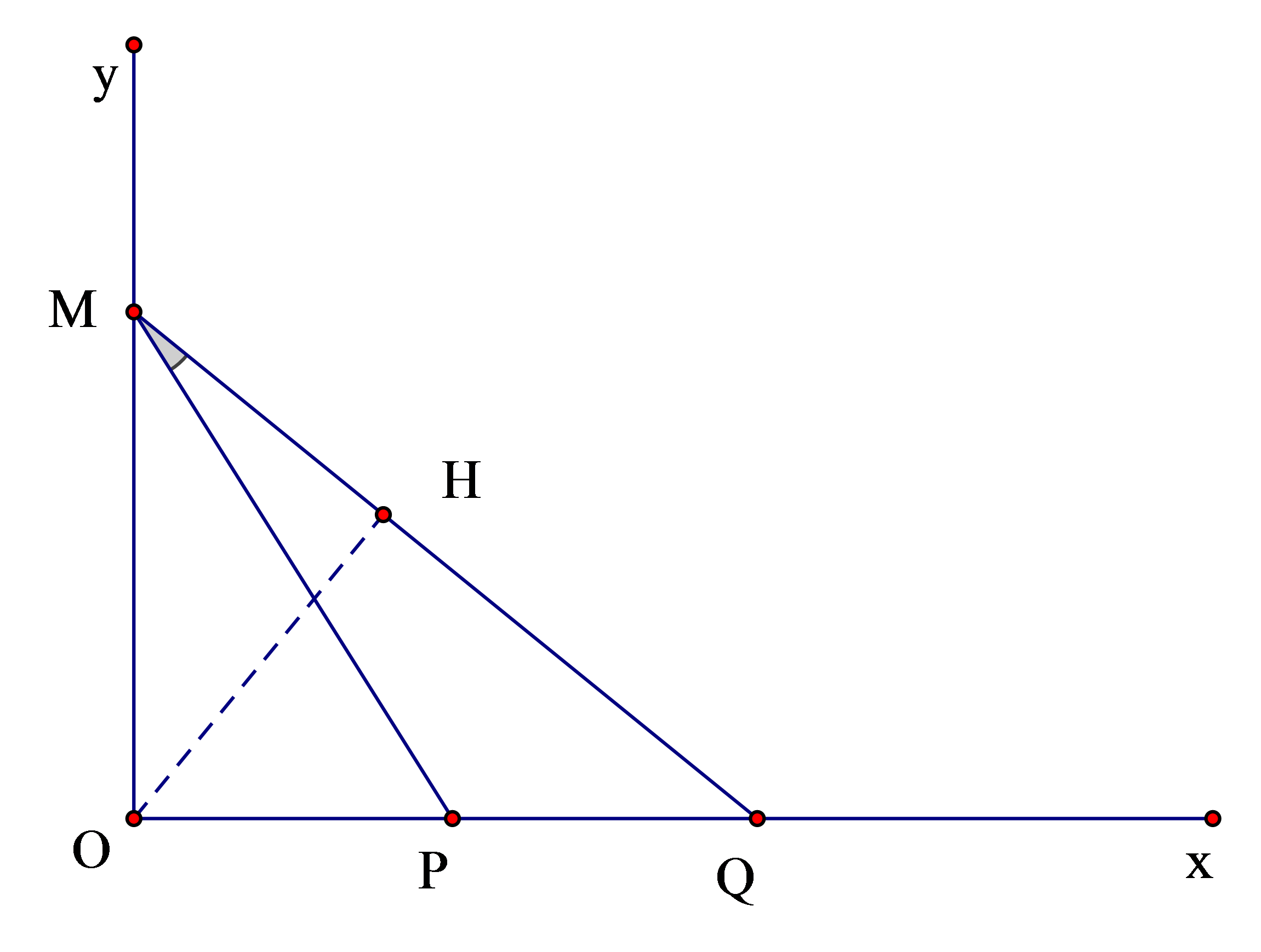
Theo đề bài ta suy ra: OP = 4,5λ, OQ = 8λ

Áp dụng định lí hàm số sin trong tam giác MPQ ta có

 \({{PQ} \over {\sin PMQ}} = {{MP} \over {\sin MQP}} = {{\sqrt {O{M^2} + O{P^2}} } \over {{{OM} \over {\sqrt {O{M^2} + O{Q^2}} }}}} = {{\sqrt {\left( {O{M^2} + O{P^2}} \right)\left( {O{M^2} + O{Q^2}} \right)} } \over {OM}}\)

Đặt OM = x ta có \({{PQ} \over {\sin PMQ}} = {{\sqrt {\left( {{x^2} + O{P^2}} \right)\left( {{x^2} + O{Q^2}} \right)} } \over x}\)

Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki cho tích  \(\left( {{x^2} + O{P^2}} \right)\left( {{x^2} + O{Q^2}} \right) \ge {\left( {OPx + OQx} \right)^2}\)

Do đó, \({{PQ} \over {\sin PMQ}} = {{\sqrt {\left( {{x^2} + O{P^2}} \right)\left( {{x^2} + O{Q^2}} \right)} } \over x} \ge {{x\left( {OP + OQ} \right)} \over x} = OP + OQ = 12,5\lambda  \Rightarrow \sin PMQ \le {{3,5} \over {12,5}}\)

Dấu “=” xảy ra ứng với góc PMQ lớn nhất khi  \({{OP} \over x} = {x \over {OQ}} \Leftrightarrow x = \sqrt {OP.OQ}  = 6\lambda \)

Do đó, OM = 6λ

* Tìm số điểm dao động ngược pha với O trên đoạn MQ

Ta tính được OH = 4,8λ

- Số điểm dao động ngược pha với nguồn trên đoạn HM là số giá trị nguyên của k thỏa mãn

 \(4,8\lambda  \le d = \left( {k + {1 \over 2}} \right)\lambda  \le 6\lambda  \Rightarrow  \le 4,3 \le k \le 5,5 \Rightarrow k = 5\)

Trên đoạn HM có 1 điểm

- Số điểm dao động ngược pha với nguồn trên đoạn HQ là số giá trị nguyên của k thỏa mãn

 \(4,8\lambda  \le d = \left( {k + {1 \over 2}} \right)\lambda  \le 8\lambda  \Rightarrow  \le 4,3 \le k \le 7,5 \Rightarrow k = 5,6,7\)

Trên đoạn HQ có 3 điểm

Vậy trên MQ có 4 điểm dao động ngược pha với O

→ Chọn B