Phương pháp giải:

Số điểm chung của đồ thị hàm số với trục hoành là số nghiệm của phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành.

Lời giải chi tiết:

Để đồ thị hàm số \(y = {x^3} + {x^2} + m\) cắt trục hoành tại đúng 1 điểm thì phương trình \({x^3} + {x^2} + m = 0\) có nghiệm duy nhất.

\({x^3} + {x^2} + m = 0 \Leftrightarrow {x^3} + {x^2} =  - m \Rightarrow \) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( x \right) = {x^3} + {x^2}\) và đường thẳng \(y =  - m\) song song với trục hoành.

Xét hàm số \(y = f\left( x \right) = {x^3} + {x^2}\) ta có \(f'\left( x \right) = 3{x^2} + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{ - 2}}{3}\end{array} \right.\)

BBT :

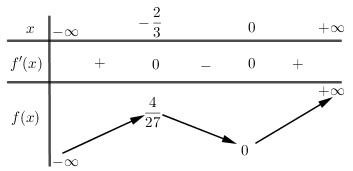
Phương trình có 1 nghiệm duy nhất \( \Leftrightarrow \left[ \begin{array}{l} - m > \frac{4}{{27}}\\ - m < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < \frac{{ - 4}}{{27}}\\m > 0\end{array} \right.\) .

Chọn đáp án B.