Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a,\)mặt bên \(SAB\) nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right),{\rm{ }}\widehat {SAB} = {30^0},{\rm{ }}SA = 2a.\) Tính thể tích \(V\) của khối chóp \(S.ABCD.\)
- A \(V = \dfrac{{\sqrt 3 {a^3}}}{6}.\)
- B \(V = {a^3}.\)
- C \(V = \dfrac{{{a^3}}}{9}.\)
- D
\(V = \dfrac{{{a^3}}}{3}.\)
Phương pháp giải:
Xác định chiều cao hình chóp \(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a \bot d;\,a \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( Q \right)\)
Thể tích khối chóp là \(V = \dfrac{1}{3}h.S\) với \(h\) là chiều cao hình chóp và \(S\) là diện tích đáy.
Lời giải chi tiết:
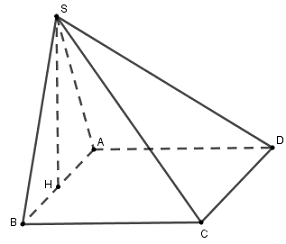
Trong \(\left( {SAB} \right)\) kẻ \(SH \bot AB\) tại \(H\)
Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \bot AB;\,SH \subset \left( {SAB} \right)\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)\)
Xét tam giác \(SAH\) có \(SH = SA.\sin \widehat {SAH} = 2a.\sin 30^\circ = a\)
Thể tích khối chóp là \(V = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}a.{a^2} = \dfrac{{{a^3}}}{3}.\)
Chọn D







