Câu hỏi
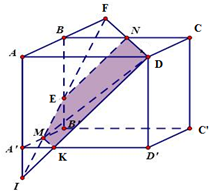
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh bằng \(1.\) Gọi \(M,N\) lần lượt là trung điểm của \(A'B'\) và\(BC.\) Mặt phẳng \((DMN)\) chia hình lập phương thành 2 phần. Gọi \({V_1}\) là thể tích của phần chứa đỉnh \(A\) và \({V_2}\) là thể tích của phần còn lại. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng
- A \(\frac{1}{2}\)
- B \(\frac{{55}}{{89}}\)
- C \(\frac{2}{3}\)
- D \(\frac{{37}}{{48}}\)
Phương pháp giải:
Sử dụng phân chia thể tích, định lý Ta-lét
Sử dụng công thức tính thể tích khối chóp chiều cao \(h\) và diện tích đáy \(S\) là \(V = \frac{1}{3}S.h\)
Thể tích hình lập phương cạnh \(a\) là \(V = {a^3}.\)
Lời giải chi tiết:
Trong mặt phẳng \(\left( {ABCD} \right)\) có \(DN\) cắt \(AB\) tại \(F.\)
Trong mặt phẳng \(\left( {ABB'A'} \right)\) có \(MF\) cắt \(AA',BB'\) lần lượt tại \(I;E.\)
Trong mặt phẳng \(\left( {ADD'A'} \right)\) có \(ID\) cắt \(A'D'\) tại \(K.\)
Như vậy mặt phẳng \(\left( {DMN} \right) \equiv \left( {DNEMK} \right)\)
Suy ra \({V_1} = {V_{ABNDKA'ME}} = {V_{I.AFD}} - {V_{E.BFM}} - {V_{IA'KM}}\)
Xét tam giác \(FAD\) có \(BN = \frac{1}{2}AD;BN//AD \Rightarrow BN\) là đường trung bình của tam giác \(FAD \Rightarrow AB = BF = 1;BN = \frac{1}{2}\)
\( \Rightarrow {S_{BNF}} = \frac{1}{2}BF.BN = \frac{1}{2}.1.\frac{1}{2} = \frac{1}{4}\) (vì \(FBN\) vuông tại \(B\)).
Lại có \(MB'//BF \Rightarrow \frac{{EB'}}{{EB}} = \frac{{MB'}}{{BF}} = \frac{{\frac{1}{2}}}{1} = \frac{1}{2} \Rightarrow \frac{{EB'}}{{BB'}} = \frac{1}{3} \Rightarrow EB' = \frac{1}{3};EB = \frac{2}{3}\)
Và \(IA'//EB' \Rightarrow \frac{{IA'}}{{EB'}} = \frac{{MA'}}{{MB'}} = 1 \Rightarrow IA' = EB' = \frac{1}{3}\)
\(A'K//AD \Rightarrow \frac{{A'K}}{{AD}} = \frac{{IA'}}{{IA}} = \frac{1}{4} \Rightarrow A'K = \frac{1}{4}\)
Suy ra \({S_{A'MK}} = \frac{1}{2}A'M.A'K = \frac{1}{2}.\frac{1}{2}.\frac{1}{4} = \frac{1}{{16}}\) (vì \(\Delta A'MK\) vuông tại \(A'\))
Lại có \({S_{AFD}} = \frac{1}{2}AF.AD = \frac{1}{2}.\left( {AB + BF} \right).AD = \frac{1}{2}.2.1 = 1\) và \(IA = IA' + AA' = \frac{1}{3} + 1 = \frac{4}{3}\)
Suy ra
\(\begin{array}{l}{V_1} = {V_{ABNDKA'ME}} = {V_{I.AFD}} - {V_{E.BFM}} - {V_{IA'KM}}\\\,\,\,\,\, = \frac{1}{3}IA.{S_{ADF}} - \frac{1}{3}.EB.{S_{BFN}} - \frac{1}{3}IA'.{S_{A'MK}}\\\,\,\,\,\, = \frac{1}{3}.\frac{4}{3}.1 - \frac{1}{3}.\frac{2}{3}.\frac{1}{4} - \frac{1}{3}.\frac{1}{3}.\frac{1}{{16}} = \frac{{55}}{{144}}\end{array}\)
Thể tích hình lập phương là \(V = 1 \Rightarrow {V_2} = V - {V_1} = 1 - \frac{{55}}{{144}} = \frac{{89}}{{144}}\)
Suy ra \(\frac{{{V_1}}}{{{V_2}}} = \frac{{55}}{{89}}.\)
Chọn B.