Phương pháp giải:

- Vẽ đồ thị hàm số \(y = {x^4} - 5{x^2} + 4\), từ đó suy ra đồ thị hàm số \(y = \left| {{x^4} - 5{x^2} + 4} \right|\).

- Sử dụng tương giao đồ thị tìm điều kiện của \(m\) thích hợp.

Lời giải chi tiết:

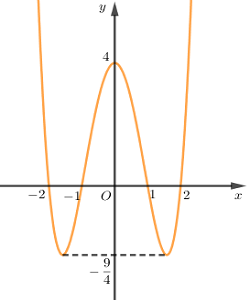
Xét hàm \(y = {x^4} - 5{x^2} + 4\) có \(y' = 4{x^3} - 10x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm \dfrac{{\sqrt {10} }}{2}\end{array} \right.\).

Suy ra đồ thị hàm số có điểm cực đại \(\left( {0;4} \right)\) và hai điểm cực tiểu \(\left( { \pm \dfrac{{\sqrt {10} }}{2}; - \dfrac{9}{4}} \right)\).

Đồ thị hàm số cắt trục \(Ox\) tại các điểm \(\left( {1;0} \right),\left( { - 1;0} \right),\left( {2;0} \right),\left( { - 2;0} \right)\).

Vẽ đồ thị:

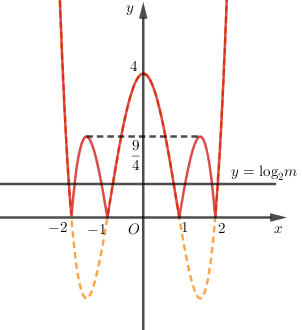
Đồ thị hàm số \(y = \left| {{x^4} - 5{x^2} + 4} \right|\) có được bằng cách:

+) Giữ nguyên phần phía trên trục \(Ox\).

+) Lấy đối xứng phần dưới trục hoành qua \(Ox\).

+) Xóa bỏ phần dưới sau khi đã lấy đổi xứng.

Khi đó ta được đồ thị như hình trên.

Dễ thấy, để phương trình \(\left| {{x^4} - 5{x^2} + 4} \right| = {\log _2}m\) có \(8\) nghiệm phân biệt thì đường thẳng \(y = {\log _2}m\) cắt đồ thị hàm số \(y = \left| {{x^4} - 5{x^2} + 4} \right|\) tại \(8\) điểm phân biệt.

\( \Leftrightarrow 0 < {\log _2}m < \dfrac{9}{4} \Leftrightarrow 1 < m < {2^{\dfrac{9}{4}}} \Leftrightarrow 1 < m < \sqrt[4]{{{2^9}}}\).

Chọn D