Câu hỏi
Cho hai tam giác \(ACD\) và \(BCD\) nằm trên hai mặt phẳng vuông góc với nhau và \(AC = AD = BC = BD = a\), \(CD = 2x\). Tìm giá trị của \(x\) để hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) vuông góc nhau.
- A \(x = \dfrac{a}{3}.\)
- B \(x = \dfrac{{a\sqrt 3 }}{3}.\)
- C \(x = \dfrac{{a\sqrt 2 }}{3}.\)
- D \(x = \dfrac{a}{2}.\)
Phương pháp giải:
Xác định góc giữa ha mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) bằng cách \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \bot d;a \subset \left( P \right)\\b \bot d;b \subset \left( Q \right)\end{array} \right. \Rightarrow \) góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) là góc giữa \(a\) và \(b.\)
Xác định chiều cao hình chóp bằng cách \(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a \bot d;a \subset \left( P \right)\end{array} \right. \Rightarrow a \bot \left( P \right)\)
Tính toán dựa vào định lý Pytago.
Lời giải chi tiết:
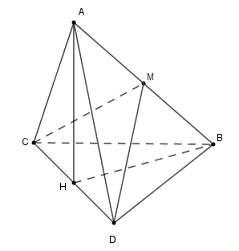
Gọi \(M\) là trung điểm \(AB\).
Vì các tam giác \(ACB,ACD\) là các tam giác cân nên \(CM \bot AB;DM \bot AB\)
Mà \(\left( {ABC} \right) \cap \left( {ABD} \right) = AB\) nên góc giữa \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) là góc \(\widehat {CMD}\).
Từ đề bài suy ra \(\widehat {CMD} = 90^\circ \)
Mà \(\Delta CAB = \Delta DAB\left( {c - c - c} \right) \Rightarrow CM = MD\).
\( \Rightarrow \Delta MCD\) vuông cân tại \(M\) có \(CD = 2x\).
\( \Rightarrow MC = MD = \dfrac{{2x}}{{\sqrt 2 }} = \sqrt 2 x\,\,\left( 1 \right)\).
Gọi \(H\) là trung điểm \(CD\) khi đó \(AH \bot CD\) (do \(ACD\) cân tại \(A\))
Mà \(\left( {ACD} \right) \bot \left( {BCD} \right);\,\left( {ACD} \right) \cap \left( {BCD} \right) = CD\) nên \(AH \bot \left( {BCD} \right)\) suy ra \(AH \bot BH\) và \(AH = BH\) (do \(\Delta ACD = \Delta BCD\left( {c - c - c} \right)\)) suy ra \(AB = BH\sqrt 2 \) , lại có theo định lý Pytago \(BH = \sqrt {B{D^2} - D{H^2}} = \sqrt {{a^2} - {x^2}} \Rightarrow AB = \sqrt {2\left( {{a^2} - {x^2}} \right)} \)\( \Rightarrow AM = \sqrt {\dfrac{{{a^2} - {x^2}}}{2}} \)
Xét tam giác vuông \(ACM\), theo định lý Pytago ta có:
\(CM = \sqrt {A{C^2} - A{M^2}} = \sqrt {{a^2} - \dfrac{{{a^2} - {x^2}}}{2}} = \sqrt {\dfrac{{{a^2} + {x^2}}}{2}} \) (2)
Từ (1) và (2) ta có \(\sqrt 2 x = \sqrt {\dfrac{{{a^2} + {x^2}}}{2}} \Leftrightarrow {a^2} + {x^2} = 4{x^2} \Leftrightarrow x = \dfrac{{a\sqrt 3 }}{3}.\)
Chọn B







