Câu hỏi
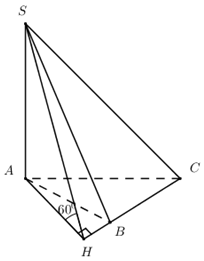
Cho hình chóp tam giác \(S.ABC\) có mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt đáy. Biết góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt đáy bằng \({60^0}\) cạnh \(AB = 4cm;\,\,BC = 6cm;\,\,CA = 8cm\). Tính độ dài cạnh SA của hình chóp.
- A \(\sqrt 5 \,cm\).
- B \(2\sqrt 3 \,cm\).
- C \(6\sqrt 3 \,cm\).
- D \(3\sqrt 5 \,cm\).
Phương pháp giải:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABC} \right)\).
Xét tam giác \(ABC\) ta có
\(\begin{array}{l}\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB.BC}} = \frac{{{4^2} + {6^2} - {8^2}}}{{2.4.6}} = - \frac{1}{4} < 0\\ \Rightarrow \angle B > {90^0}\end{array}\)
Trong \(\left( {ABC} \right)\) dựng \(AH \bot BC\,\,\left( {H \in BC} \right)\) ta có:
\(\left\{ \begin{array}{l}BC \bot AH\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\).
\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SH \bot \left( {ABC} \right)\\\left( {ABC} \right) \supset AH \bot \left( {ABC} \right)\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABC} \right)} \right) = \angle \left( {SH;AH} \right) = \angle SHA = {60^0}\).
Xét tam giác vuông \(AHB\) có \(BH = AB.\cos \angle ABH = 4.\frac{1}{4} = 1\).
\( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{4^2} - {1^2}} = \sqrt {15} \).
Xét tam giác vuông \(SAH\) có : \(SA = AH.\tan {60^0} = \sqrt {15} .\sqrt 3 = 3\sqrt 5 \).
Chọn D.