Câu hỏi
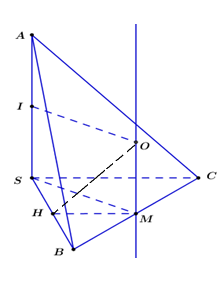
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và \(SA = SC = a\),\(SB = 2a\). Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABGóc giữa hai mặt phẳng (SBO) và (SBC) bằng
- A \({30^0}\)
- B \({90^0}\)
- C \({60^0}\)
- D \({45^0}\)
Phương pháp giải:
+) Xác định tâm \(O\) của mặt cầu ngoại tiếp khối chóp \(SABC.\)
+) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng thuộc hai mặt phẳng cùng vuông góc với giao tuyến.
Lời giải chi tiết:
Ta có: \(\Delta SBC\) vuông tại \(S \Rightarrow M\) là tâm đường tròn ngoại tiếp \(\Delta SBC\) với \(M\) là trung điểm của \(BC.\)
Gọi \(I,\,\,H\) lần lượt là trung điểm của các cạnh \(SA,\,\,SC.\)
Qua \(M,\) dựng đường thẳng \(d//SA\)
Qua \(I,\,\,\) dựng đường thẳng song song với \(SM,\) cắt \(d\) tại \(O.\)
\( \Rightarrow O\) là tâm mặt cầu ngoại tiếp khối chóp \(SABC.\)
Ta có: \(\left( {SBO} \right) \cap \left( {SBC} \right) = SB.\)
Ta có: \(\left\{ \begin{array}{l}SB \bot OM\\SB \bot HM\end{array} \right. \Rightarrow SB \bot \left( {OMH} \right) \Rightarrow SB \bot OH.\)
Có: \(\left\{ \begin{array}{l}MH \bot SB\,\,\left( {MH//SC} \right)\\OH \bot SB\,\,\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow \angle \left( {\left( {SBO} \right),\,\left( {SBC} \right)} \right) = \angle \left( {MH,\,OH} \right) = \angle OHM\)
Xét \(\Delta OHM\) vuông tại \(M\) ta có: \(\tan OHM = \dfrac{{OM}}{{HM}} = \dfrac{{\dfrac{1}{2}SA}}{{\dfrac{1}{2}SC}} = \dfrac{{SA}}{{SC}} = \dfrac{a}{a} = 1 \Rightarrow \angle OHM = {45^0}.\)
Chọn D.