Câu hỏi
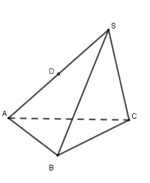
Hình chóp đều \(S.ABCD\) có \(SA = AB = a\). Cosin góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) bằng
- A \(\dfrac{{\sqrt 2 }}{2}\)
- B \( - \dfrac{{\sqrt 2 }}{2}\)
- C \(\dfrac{1}{3}\)
- D \( - \dfrac{1}{3}\)
Phương pháp giải:
Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
Lời giải chi tiết:
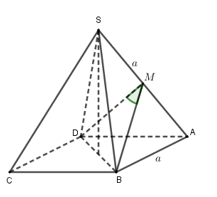
Gọi \(M\) là trung điểm của \(SA\).
Do \(S.ABCD\) đều nên \(SA = SB = SC = SD\). Mà \(SA = AB = a\) nên các tam giác \(SAB,SAD\) là tam giác đều.
Khi đó \(BM \bot SA,DM \bot SA\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAD} \right) = SA\\BM \subset \left( {SAB} \right),DM \subset \left( {SAD} \right)\\BM \bot SA,DM \bot SA\end{array} \right.\) \( \Rightarrow \) góc giữa \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) bằng \(\widehat {\left( {BM,DM} \right)} = \widehat {BMD}\).
Dễ thấy \(BM = DM = \dfrac{{a\sqrt 3 }}{2},BD = a\sqrt 2 \).
\( \Rightarrow \cos \widehat {BMD} = \dfrac{{B{M^2} + D{M^2} - B{D^2}}}{{2BM.DM}}\) \( = \dfrac{{\dfrac{{3{a^2}}}{4} + \dfrac{{3{a^2}}}{4} - 2{a^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2}}} = - \dfrac{1}{3}\).
Chọn D.