Phương pháp giải:

Tính \(y'\) rồi gpt \(y' = 0\) rồi lập BBT đếm số cực trị

Lời giải chi tiết:

ĐK : \(x \in \mathbb{R}\) . Ta có \(y' = \dfrac{2}{5}.\dfrac{1}{{\sqrt[5]{{{x^3}}}}} - 1\)

Giải phương trình \(y' = 0 \Leftrightarrow \dfrac{2}{5}\dfrac{1}{{\sqrt[5]{{{x^3}}}}} - 1 = 0\,\,\left( {x \ne 0} \right) \Leftrightarrow \sqrt[5]{{{x^3}}} = \dfrac{5}{2} \Leftrightarrow x = \sqrt[3]{{{{\left( {\dfrac{5}{2}} \right)}^5}}}\)

Ta có BBT :

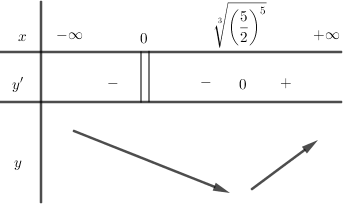
Vậy hàm số đã cho có 1 cực trị.

Chọn A