Câu hỏi
Nếu hàm số\(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f(x) > f\left( 0 \right)_{}^{}\forall x \in \left( { - 1;1} \right)\backslash \left\{ 0 \right\}\) thì:
- A Hàm số đạt cực tiểu tại \(x = 1\).
- B Hàm số đạt cực tiểu tại \(x = 0\).
- C Hàm số đạt cực đại tại \(x = - 1\).
- D Hàm số đạt GTNN trên tập số thực tại \(x = 0\).
Phương pháp giải:
Theo bài toán suy ra BBT của đồ thị hàm số \(y = f\left( x \right)\) và kết luận.
Lời giải chi tiết:
Theo bài toán ta có thể suy ra BBT của đồ thị hàm số \(y = f\left( x \right)\) như sau:
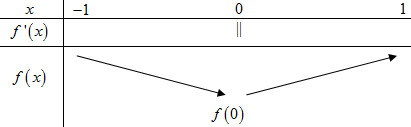
Dễ thấy các đáp án A, C, D đều sai. Hàm số đạt cực tiểu tại \(x = 0\).
Chọn B.
Câu hỏi trước
