Phương pháp giải:

Phân chia khối đa diện và sử dụng các công thức tính thể tích khối chóp \(V = \dfrac{1}{3}h.S\) và thể tích lăng trụ \(V = h.S\) với \(h\) là chiều cao của khối đa diện và \(S\) là diện tích đáy. Từ đó tính thể tích các khối chóp theo thể tích lăng trụ rồi so sánh.

Sử dụng nếu \(a//\left( P \right)\) thì \(d\left( {A;\left( P \right)} \right) = d\left( {B;\left( P \right)} \right)\) với \(A,B \in a\).

Lời giải chi tiết:

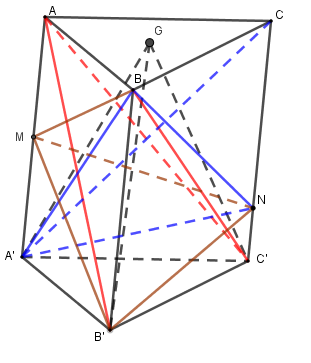
+ Gọi chiều cao lăng trụ là \(h\) và diện tích đáy là \(S = {S_{ABC}} = {S_{A'B'C'}}\) thì thể tích khối lăng trụ \(ABC.A'B'C'\) là \(V = h.S\)

+ Xét khối chóp \(G.A'B'C'\) có \({V_{G.A'B'C'}} = \dfrac{1}{3}d\left( {G;\left( {A'B'C'} \right)} \right).{S_{A'B'C'}} = \dfrac{1}{3}h.S = \dfrac{V}{3}\)  (1)

+ Xét khối chóp \(C'.ABC\) có \({V_{C'ABC}} = \dfrac{1}{3}h\left( {C';\left( {ABC} \right)} \right).{S_{ABC}} = \dfrac{1}{3}h.S = \dfrac{V}{3}\)  nên

\({V_{C'.ABB'A'}} = \dfrac{2}{3}V\left( { = \dfrac{1}{3}d\left( {C';\left( {ABB'A'} \right)} \right).{S_{ABB'A'}}} \right)\)

Lại có

     \(\begin{array}{l}{V_{ABB'C'}} = \dfrac{1}{3}d\left( {C';\left( {ABB'A'} \right)} \right).{S_{ABB'}} = \dfrac{1}{2}.\dfrac{1}{3}d\left( {C';\left( {ABB'A'} \right)} \right).{S_{ABB'A'}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}{V_{C'.ABB'A'}} = \dfrac{1}{2}.\dfrac{{2V}}{3} = \dfrac{V}{3}\,\,\left( 2 \right)\end{array}\).

+)  Xét khối chóp \(BB'MN\) có \({S_{MBB'}} = \dfrac{1}{2}{S_{ABB'A'}}\) (có cùng cạnh đáy \(BB'\)  và chiều cao bằng nhau)

     \(\begin{array}{l}{V_{N.BB'M}} = \dfrac{1}{3}d\left( {N;\left( {BB'A'A} \right)} \right).{S_{MBB'}} = \dfrac{1}{3}d\left( {C';\left( {BB'A'A} \right)} \right).\dfrac{1}{2}{S_{ABB'A'}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}{V_{C'.ABB'A'}} = \dfrac{1}{2}.\dfrac{{2V}}{3} = \dfrac{V}{3}\end{array}\) (3)

+)  Xét khối chóp \(A'BCN\) có \({S_{BCN}} = \dfrac{1}{2}d\left( {B;CC'} \right).CN = \dfrac{1}{2}d\left( {B;CC'} \right).\dfrac{4}{5}CC' = \dfrac{4}{5}.{S_{BCC'}}\)

Khi đó

     \(\begin{array}{l}{V_{A'.BCN}} = \dfrac{1}{3}d\left( {A';\left( {BCC'B'} \right)} \right).{S_{BCN}} = \dfrac{1}{3}d\left( {A';\left( {BCC'B'} \right)} \right).\dfrac{4}{5}{S_{BCC'}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{4}{5}\left( {\dfrac{1}{3}d\left( {A';\left( {BCC'B'} \right)} \right).{S_{BCC'}}} \right) = \dfrac{4}{5}{V_{A'.BCC'}} = \dfrac{4}{5}.\dfrac{1}{2}{V_{A'.BCC'B'}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{2}{5}.\left( {V - {V_{A'.ABC}}} \right) = \dfrac{2}{5}\left( {V - \dfrac{V}{3}} \right) = \dfrac{V}{5}\,\,\left( 4 \right)\end{array}\)

Từ (1), (2), (3), (4) suy ra khối tứ diện có thể tích nhỏ nhất là \(A'BCN\).

Chọn B