Câu hỏi
Người ta gọt một khối lập phương gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương). Biết các cạnh của khối lập phương bằng a. Hãy tính thể tích của khối tám mặt đều đó.
- A \(\dfrac{{{a^3}}}{6}\)
- B \(\dfrac{{{a^3}}}{{12}}\)
- C \(\dfrac{{{a^3}}}{4}\)
- D \(\dfrac{{{a^3}}}{8}\)
Phương pháp giải:
Xác định cạnh của khối bát diện đều và tính thể tích theo công thức \(V = \dfrac{{{a^3}\sqrt 2 }}{3}\) với \(a\) là độ dài cạnh hình bát diện đều.
Lời giải chi tiết:
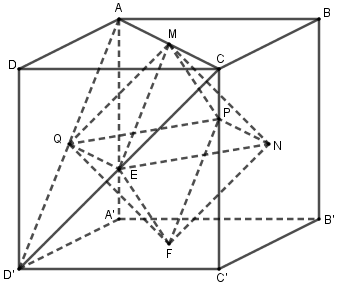
Xét hình lập phương \(ABCD.A'B'C'D\) cạnh \(a\) và khối bát diện đều nội tiếp \(MNPQEF\).
Ta có: \(ME\) là đường trung bình của tam giác \(CAD'\) nên \(ME = \dfrac{1}{2}AD' = \dfrac{{a\sqrt 2 }}{2}\).
Vậy thể tích \({V_{MNPQEF}} = \dfrac{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^3}.\sqrt 2 }}{3} = \dfrac{{{a^3}}}{6}\).
Chọn A
Câu hỏi trước
