Môn Lý - Lớp 12
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
Câu hỏi
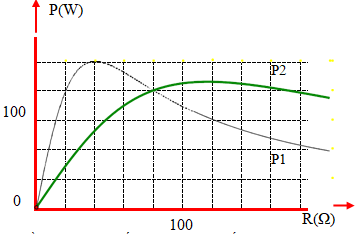
Trong mạch điện xoay chiều RLC nối tiếp, với R là một biến trở. Đặt vào hai đầu lần lượt các điện áp u1 = U01.cosω1t và u2 = U02.cosω2t thì công suất tiêu thụ trên mạch tương ứng là P1 và P2 phụ thuộc vào giá trị biến trở R như hình vẽ. Hỏi khi P1 đạt cực đại thì P2 có giá trị là:
- A 120,5 W
- B 120,0 W
- C 130,5 W
- D 130,0 W
Phương pháp giải:
Áp dụng công thức tính công suất
\(P = {I^2}.R = \frac{{{U^2}}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}.R\)
Lời giải chi tiết:
Áp dụng công thức tính công suất
\(\begin{array}{l}
P = {I^2}.R = \frac{{{U^2}}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}.R = \frac{{{U^2}}}{{R + \frac{{{{({Z_L} - {Z_C})}^2}}}{R}}}\\
= > {P_{\max }} \Leftrightarrow {R^2} = {({Z_L} - {Z_C})^2} \Rightarrow P = \frac{{{U^2}}}{{2R}}
\end{array}\)
Từ đồ thị ta thấy P1 cực đại khi R = 40Ω
Thay vào biểu thức P cực đại ta được
\(250 = \frac{{U_1^2}}{{2.40}} \Rightarrow {U_1} = \sqrt {20000} V\)
Với hai giá trị R = 40Ω và R = 80 Ω thì P1 cùng có giá trị 200W
Ta có:
\(\begin{array}{l}
\frac{{U_1^2.20}}{{{{20}^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \frac{{U_1^2.80}}{{{{80}^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}}\\
\Rightarrow |{Z_{L1}} - {Z_{C1}}| = 40\Omega
\end{array}\)
Với hai giá trị R = 80 và R = 180 thì P2 có cùng giá trị 200W
Nên ta có:
\(\begin{array}{l}
\frac{{U_2^2.80}}{{{{80}^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \frac{{U_2^2.180}}{{{{180}^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}}\\
\Rightarrow \left| {{Z_{L1}} - {Z_{C1}}} \right| = 120\Omega
\end{array}\)
Với hai giá trị R = 80 Ω thì P1 = P2 = 200W
Ta có:
\(\begin{array}{l}
\frac{{U_1^2.80}}{{{{80}^2} + {{({Z_{L1}} - {Z_{C1}})}^2}}} = \frac{{U_2^2.80}}{{{{80}^2} + {{({Z_{L2}} - {Z_{C2}})}^2}}}\\
\Rightarrow \frac{{20000}}{{{{80}^2} + {{40}^2}}} = \frac{{U_2^2}}{{{{80}^2} + {{120}^2}}} \Rightarrow {U_2} = \sqrt {52000} V
\end{array}\)
Khi R = 40Ω thì P2có giá trị là
\({P_2} = \frac{{52000.40}}{{{{40}^2} + {{120}^2}}} = 130W\)
Câu hỏi trước
