Phương pháp giải:

Sử dụng tính chất của tứ diện vuông.

Lời giải chi tiết:

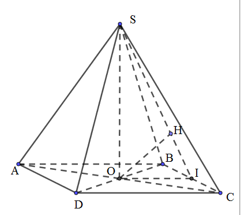
Gọi O là tâm hình vuông ABCD, I là trung điểm của BC. Dựng \(OH \bot SI,\,\left( {H \in SI} \right)\)

Ta có:  \(\left\{ \begin{array}{l}BC \bot SO\\BC \bot SI\end{array} \right. \Rightarrow BC \bot \left( {SOI} \right) \Rightarrow BC \bot OH\)

Mà \(SI \bot OH \Rightarrow OH \bot \left( {SBC} \right)\)

Do \(\left\{ \begin{array}{l}AC \cap \left( {SBC} \right) = \left\{ C \right\}\\AC = 2.OC\end{array} \right. \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = 2.d\left( {O;\left( {SBC} \right)} \right) = 2.OH = 2a \Rightarrow OH = a\)

Ta có: \({V_{S.ABCD}} = 4.{V_{O.SBC}}\)

Giả sử tứ diện vuông S.OBC có: \(OB = OC = x,\,\,SO = y\,\,\left( {x,y > 0} \right)\).

Khi đó: \({V_{O.SBC}} = \dfrac{{SO.OB.OC}}{6} = \dfrac{{{x^2}y}}{6}\) và

\(\dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} + \dfrac{1}{{S{O^2}}} = \dfrac{1}{{O{H^2}}} \Leftrightarrow \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} = \dfrac{1}{{{a^2}}}\)

Áp dụng BĐT Cô si:

\(\dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} \ge \dfrac{3}{{\sqrt[3]{{{{\left( {{x^2}y} \right)}^2}}}}} \Rightarrow \dfrac{1}{{{a^2}}} \ge \dfrac{3}{{\sqrt[3]{{{{\left( {{x^2}y} \right)}^2}}}}} \Leftrightarrow \dfrac{{\sqrt[3]{{{{\left( {{x^2}y} \right)}^2}}}}}{3} \ge {a^2} \Leftrightarrow {x^2}y \ge 3\sqrt 3 {a^3}\)

\( \Rightarrow {V_{O.SBC}} = \dfrac{{{x^2}y}}{6} \ge \dfrac{{3\sqrt 3 {a^3}}}{6} = \dfrac{{\sqrt 3 {a^3}}}{2}\)\( \Rightarrow {V_{S.ABCD}} \ge 2\sqrt 3 {a^3}\)

Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}x = y\\\dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} = \dfrac{1}{{{a^2}}}\end{array} \right. \Leftrightarrow x = y = \dfrac{a}{{\sqrt 3 }}\)

Khối chóp \(S.ABCD\) có thể tích nhỏ nhất bằng \(2\sqrt 3 {a^3}\).

Chọn: A