Câu hỏi
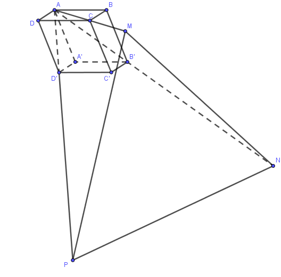
Cho khối hộp \(ABCD.A'B'C'D'\) có thể tích \(V\). Các điểm \(M,N,P\) thỏa mãn \(\overrightarrow {AM} = 2\overrightarrow {AC} \), \(\overrightarrow {AN} = 3\overrightarrow {AB'} \), \(\overrightarrow {AP} = 4\overrightarrow {AD'} \). Tính thể tích khối chóp \(AMNP\) theo \(V\).
- A \(6V\).
- B \(8V\).
- C \(12V\).
- D \(4V\).
Phương pháp giải:
Tính tỉ số thể tích giữa khối chóp \(AMNP\) và thể tích khối hộp \(ABCD.A'B'C'D'\).
Lời giải chi tiết:
Ta có: \(\dfrac{{{V_{AMNP}}}}{{{V_{ACB'D'}}}} = \dfrac{{AM}}{{AC}}.\dfrac{{AN}}{{AB'}}.\dfrac{{AP}}{{AD'}} = 2.3.4 = 24 \Rightarrow {V_{AMNP}} = 24{V_{ACB'D'}}\)
Mà \({V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} - {V_{D.ACD'}} - {V_{B.ACB'}} - {V_{A'.AB'D'}} - {V_{C'.CD'B'}} = V - 4.\dfrac{1}{6}V = \dfrac{1}{3}V\)
\( \Rightarrow {V_{AMNP}} = 24.\dfrac{1}{3}V = 8V\).
Chọn: B
Câu hỏi trước
