Phương pháp giải:

Biểu diễn hình học của số phức.

Lời giải chi tiết:

\(\left| {z - 2 - 3i} \right| = 5 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \({z_1},{z_2}\) là đường tròn \(\left( {I\left( {2;3} \right);R = 5} \right)\)

Giả sử \(A,B\) lần lượt là điểm biểu diễn số phức \({z_1},{z_2}\). Do \(\left| {{z_1} - {z_2}} \right| = 6 \Rightarrow AB = 6\).

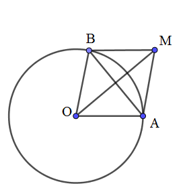
Khi đó, \(w = {z_1} + {z_2}\) có điểm biểu diễn M là đỉnh thứ tư của hình bình hành AOBM.

Ta có: \(\cos \widehat {BOA} = \dfrac{{O{B^2} + O{A^2} - A{B^2}}}{{2.OB.OA}} = \dfrac{{{5^2} + {5^2} - {6^2}}}{{2.5.5}} = \dfrac{7}{{25}} \Rightarrow \cos \widehat {OBM} =  - \dfrac{7}{{25}}\)

\(O{M^2} = O{B^2} + B{M^2} - 2.OB.BM.\cos \widehat {OBM} = {5^2} + {5^2} - 2.5.5.\dfrac{{ - 7}}{{25}} = 64 \Rightarrow OM = 8\)

Vậy, tập hợp các điểm M biểu diễn số phức \(w = {z_1} + {z_2}\) là đường tròn tâm O bán kính 8.

Chọn: A