Câu hỏi
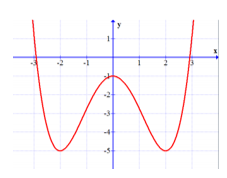
Đường cong trong hình vẽ bên là đồ thị của một trong 4 hàm số dưới đây. Hỏi hàm số đó là hàm số nào?
- A \(y = - \dfrac{{{x^4}}}{4} + {x^2} - 1\).
- B \(y = \dfrac{{{x^4}}}{4} - 2{x^2} - 1\).
- C \(y = \dfrac{{{x^4}}}{4} - {x^2} - 1\).
- D \(y = \dfrac{{{x^4}}}{4} - \dfrac{{{x^2}}}{2} - 1\).
Phương pháp giải:
Nhận biết đồ thị hàm số bậc bốn trùng phương.
Lời giải chi tiết:
Quan sát đồ thị hàm số, ta thấy: khi \(x \to + \infty \) thì \(y \to + \infty \) nên hệ số \(a > 0 \Rightarrow \) Loại phương án A
Hàm số có 3 điểm cực trị là \(A\left( {0; - 1} \right),\,B\left( { - 2; - 5} \right),C\left( {2;5} \right) \Rightarrow \) Chọn B. \(y = \dfrac{{{x^4}}}{4} - 2{x^2} - 1\)
(do \(y = \dfrac{{{x^4}}}{4} - 2{x^2} - 1 \Rightarrow y' = {x^3} - 4x\) có 3 nghiệm phân biệt là \(0; - 2;2\), còn các hàm số của phương án C và D thì không).
Chọn: B
Câu hỏi trước
