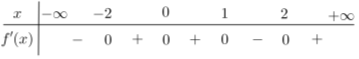Phương pháp giải:

Sử dụng công thức tính đạo hàm hàm hợp \({\left( {f\left( u \right)} \right)^\prime } = u'.f'\left( u \right)\)

Hàm số \(y = f\left( x \right)\) nghịch biến trên \(K\) nếu \(f\left( x \right) \le 0;\,\forall x \in K\) và \(f'\left( x \right) = 0\) xảy ra tại hữu hạn điểm.

Lời giải chi tiết:

Xét hàm số \(y = f\left( {4 - x} \right) - x + \sqrt {{x^2} + 1} \) có \(y' =  - f\left( {4 - x} \right) - 1 + \frac{x}{{\sqrt {{x^2} + 1} }}\)

Ta có  \(y' < 0 \Leftrightarrow  - f\left( {4 - x} \right) - 1 + \frac{x}{{\sqrt {{x^2} + 1} }} < 0 \Leftrightarrow f\left( {4 - x} \right) > 1 - \frac{x}{{\sqrt {{x^2} + 1} }}\) 

Nhận thấy \(1 - \frac{x}{{\sqrt {{x^2} + 1} }} = \frac{{\sqrt {{x^2} + 1}  - x}}{{\sqrt {{x^2} + 1} }} > 0;\,\forall x\,\,\,\left( {do\,\,\sqrt {{x^2} + 1}  > \left| x \right| \ge x\,\,\forall x} \right)\)

Nên suy ra \(f\left( {4 - x} \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - 2 < 4 - x < 1\\4 - x > 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3 < x < 6\\x < 2\end{array} \right.\)

Vậy hàm số nghịch biến trên khoảng \(\left( {3;6} \right)\)

Chọn B.