Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
Câu hỏi
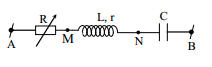
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch AB (hình bên). Điều chỉnh R đến giá trị 80 Ω thì công suất tiêu thụ trên biến trở đạt cực đại, đồng thời tổng trở của đoạn mạch AB là số nguyên nhỏ nhất và chia hết cho 40. Khi đó, hệ số công suất của đoạn mạch AB có giá trị là
- A 0,25
- B 0,125
- C 0,75
- D 0,625
Phương pháp giải:
Tổng trở mạch có RLrC là \(Z=\sqrt{{{(R+r)}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\)
Biểu thức định luật Ôm cho đoạn mạch: I = U/Z
Công suất tiêu thụ trên điện trở R là P = I2R
Hệ số công suất đoạn mạch: cosφ = R/Z
Lời giải chi tiết:
Công suất tiêu thụ trên biến trở R là:
\(P={{I}^{2}}R=\frac{{{U}^{2}}R}{{{Z}^{2}}}=\frac{{{U}^{2}}R}{{{(R+r)}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}=\frac{{{U}^{2}}}{2r+R+\frac{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R}}\)
Để P max thì mẫu số nhỏ nhất. Áp dụng BĐT Cô si cho hai số không âm ta có:
\(R+\frac{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}{R}\ge 2\sqrt{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\)
Vậy mẫu số nhỏ nhất bằng \(2r+2\sqrt{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\) khi \(R=\sqrt{{{r}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}=80\Omega \)
Tổng trở mạch điện khi đó là:
\(Z=\sqrt{{{(R+r)}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}=\sqrt{{{(80+r)}^{2}}+{{80}^{2}}-{{r}^{2}}}=\sqrt{{{2.80}^{2}}+160r}\)
Để Z chia hết cho 40 thì \(\frac{{{Z}^{2}}}{{{40}^{2}}}=8+\frac{r}{10}\) là số nguyên và r nhỏ nhất => r = 10Ω => Z = 120Ω
Hệ số công suất đoạn mạch AB là: \(\cos \varphi =\frac{R+r}{Z}=\frac{80+10}{120}=0,75\)
Chọn C