Câu hỏi
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có bảng biến thiên:
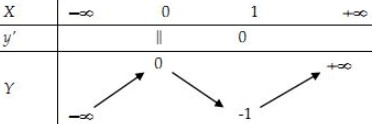
Khẳng định nào sau đây là khẳng định đúng:
- A Hàm số có giá trị cực tiểu bằng 1.
- B Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng –1.
- C Hàm số đạt cực đại tại x= 0 và đạt cực tiểu tại x=1.
- D Hàm số có đúng một cực trị.
Phương pháp giải:
Dựa vào BBT để suy ra số điểm cực trị của hàm số.
Lời giải chi tiết:
Dựa vào bảng bảng biến thiên, ta thấy\(\forall x \in \left( {--1;{\rm{ }}1} \right)\), ta có \(f\left( x \right){\rm{ }} < {\rm{ }}f\left( 0 \right)\)⇒ Hàm số đạt cực đại tại\(x = 0\).
\(\forall x \in \left( {0;2} \right),\) ta có \(f\left( x \right){\rm{ }} > {\rm{ }}f\left( 1 \right)\)⇒ Hàm số đạt cực tiểu tại \(x = 1\).
Hàm số có 2 điểm cực trị \(x = 0\) và \(x = 1\).
Vì giới hạn tại vô cực của hàm số là ±∞ nên hàm số không có giá trị lớn nhất và nhỏ nhất.
Chọn C.







