Phương pháp giải:

Điểm \(x_0\) là điểm cực tiểu của hàm số \(y=f(x)\) \( \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right..\)

Lời giải chi tiết:

Ta có: \(y' = m + \dfrac{x}{{\sqrt {{x^2} + 1} }}\)

Để giải nhanh bài toán này, ta thử với từng giá trị của \(m\) để loại trừ đáp án.

+) Trước hết ta thử với \(m = 0\).

Với \(m = 0\) thì \(y' = 0 \Leftrightarrow x = 0\)

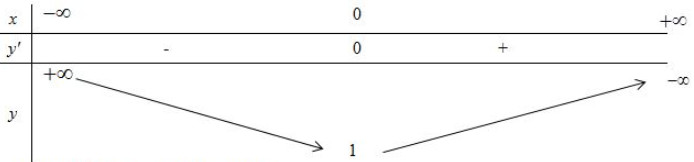
\( \Rightarrow m = 0\) thỏa mãn \( \Rightarrow \) loại đáp án D.

+) Thử với giá trị \(m = 1\) ta được: \(y' = 0 \Leftrightarrow 1 + \dfrac{x}{{\sqrt {{x^2} + 1} }} = 0 \Leftrightarrow \sqrt {{x^2} + 1}  =  - x\)\( \Rightarrow \) pt vô nghiệm.

\( \Rightarrow m = 1\) không thỏa mãn \( \Rightarrow \) loại đáp án C.

+) Thử với giá trị \(m =  - \dfrac{1}{2}\) ta được: \(y' = 0 \Leftrightarrow  - \dfrac{1}{2} + \dfrac{x}{{\sqrt {{x^2} + 1} }} = 0 \Leftrightarrow {x^2} = \dfrac{1}{3} \Leftrightarrow x =  \pm \dfrac{1}{{\sqrt 3 }}\)

\( \Rightarrow \) hàm số có cực tiểu \( \Rightarrow \) loại B.

Chọn A.