Phương pháp giải:

- Gọi tọa độ điểm \(M\) thuộc đồ thị hàm số.

- Tính khoảng cách từ \(M\) đến \(AB\) suy ra diện tích.

- Từ đó sử dụng phương pháp hàm số tìm GTLN của diện tích tam giác \(ABM\).

Lời giải chi tiết:

Ta có: \(A\left( {0; - 7} \right),B\left( {3; - 1} \right)\) \( \Rightarrow AB = 3\sqrt 5 \).

Phương trình đường thẳng \(AB:\dfrac{{x - 0}}{{3 - 0}} = \dfrac{{y + 7}}{{ - 1 + 7}} \Leftrightarrow 2x - y - 7 = 0\).

Gọi \(M\left( {{x_M};\dfrac{{{x_M} - 7}}{{{x_M} + 1}}} \right) \in \left( C \right)\) với \(0 < {x_M} < 3\)

\( \Rightarrow d\left( {M,AB} \right) = \dfrac{{\left| {2{x_M} - \dfrac{{{x_M} - 7}}{{{x_M} + 1}} - 7} \right|}}{{\sqrt {{2^2} + {1^2}} }}\) \( = \dfrac{{\left| {2{x_M} - 8 + \dfrac{8}{{{x_M} + 1}}} \right|}}{{\sqrt 5 }}\)

\( \Rightarrow {S_{MAB}} = \dfrac{1}{2}AB.d\left( {M,AB} \right)\) \( = \dfrac{1}{2}.3\sqrt 5 .\dfrac{{\left| {2{x_M} - 8 + \dfrac{8}{{{x_M} + 1}}} \right|}}{{\sqrt 5 }}\) \( = 3\left| {{x_M} - 4 + \dfrac{4}{{{x_M} + 1}}} \right|\)

Xét \(g\left( {{x_M}} \right) = {x_M} - 4 + \dfrac{4}{{{x_M} + 1}}\) với \(0 < {x_M} < 3\) ta có:

\(g'\left( {{x_M}} \right) = 1 - \dfrac{4}{{{{\left( {{x_M} + 1} \right)}^2}}} = \dfrac{{{{\left( {{x_M} + 1} \right)}^2} - 4}}{{{{\left( {{x_M} + 1} \right)}^2}}} = \dfrac{{\left( {{x_M} + 3} \right)\left( {{x_M} - 1} \right)}}{{{{\left( {{x_M} + 1} \right)}^2}}} = 0 \Leftrightarrow {x_M} = 1\)

Bảng biến thiên:

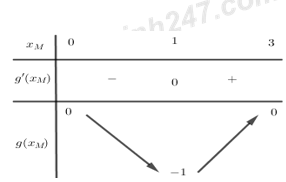
Do đó \( - 1 \le g\left( {{x_M}} \right) < 0 \Rightarrow 0 < \left| {g\left( x \right)} \right| \le 1\) \( \Rightarrow {S_{MAB}} = 3.\left| {g\left( {{x_M}} \right)} \right| \le 3.1 = 3\).

Vậy \({S_{MAB}}\) đạt GTLN bằng \(3\) tại \({x_M} = 1\).

Chọn A.