Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
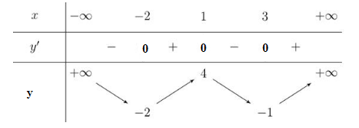
Khẳng định nào sau đây sai?
- A \(\mathop {\min }\limits_{\left[ {1;3} \right]} f\left( x \right) = - 1\)
- B \(\mathop {\max }\limits_\mathbb{R} f\left( x \right) = 4\)
- C \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = - 2\)
- D \(\mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = 4\)
Phương pháp giải:
Đọc bảng biến thiên để suy ra GTLN và GTNN của hàm số
Lời giải chi tiết:
Từ BBT ta thấy \(\mathop {\min }\limits_{\left[ {1;3} \right]} f\left( x \right) = - 1;\) \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = - 2;\)\(\mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = 4\) là những khẳng định đúng.
Còn đáp án B : \(\mathop {\max }\limits_\mathbb{R} f\left( x \right) = 4\) sai vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \) nên không tồn tại GTLN của hàm số trên \(\mathbb{R}.\)
Chọn B.







