Câu hỏi
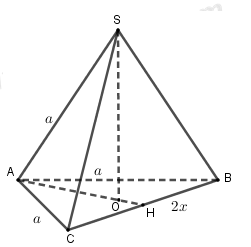
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = AB = AC = a,BC = 2x\) (trong đó \(a\) là hằng số và \(x\) thay đổi thuộc khoảng \(\left( {0;\dfrac{{a\sqrt 3 }}{2}} \right)\)). Tính thể tích lớn nhất \({V_{\max }}\) của hình chóp \(S.ABC\).
- A \({V_{\max }} = \dfrac{{{a^3}}}{6}\)
- B \({V_{\max }} = \dfrac{{{a^3}\sqrt 2 }}{4}\)
- C \({V_{\max }} = \dfrac{{{a^3}}}{8}\)
- D \({V_{\max }} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Phương pháp giải:
- Lập hàm số tính thể tích \(V\) theo \(x\).
- Sử dụng phương pháp xét hàm tìm \({V_{\max }}\).
Lời giải chi tiết:
Gọi \(O\) la tâm đường tròn ngoại tiếp tam giác \(ABC\) thì \(O \in AH\) với \(H\) là trung điểm \(BC\).
Do \(SA = SB = SC\) nên \(SO \bot \left( {ABC} \right)\).
Tam giác \(AHB\) vuông tại \(H\) có \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - {x^2}} \).
Diện tích \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}\sqrt {{a^2} - {x^2}} .2x = x\sqrt {{a^2} - {x^2}} \).
Ta có: \(AO = R = \dfrac{{AB.AC.BC}}{{4{S_{ABC}}}} = \dfrac{{a.a.2x}}{{4x\sqrt {{a^2} - {x^2}} }} = \dfrac{{{a^2}}}{{2\sqrt {{a^2} - {x^2}} }}\).
Tam giác \(SAO\) vuông tại \(O\) có \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{a^2} - \dfrac{{{a^4}}}{{4\left( {{a^2} - {x^2}} \right)}}} \) \( = \sqrt {\dfrac{{4{a^4} - 4{a^2}{x^2} - {a^4}}}{{4\left( {{a^2} - {x^2}} \right)}}} = \dfrac{{a\sqrt {3{a^2} - 4{x^2}} }}{{2\sqrt {{a^2} - {x^2}} }}\)
Thể tích khối chóp \(V = \dfrac{1}{3}{S_{ABC}}.SO\) \( = \dfrac{1}{3}x\sqrt {{a^2} - {x^2}} .\dfrac{{a\sqrt {3{a^2} - 4{x^2}} }}{{2\sqrt {{a^2} - {x^2}} }}\) \( = \dfrac{{ax\sqrt {3{a^2} - 4{x^2}} }}{6}\).
Xét hàm \(y = f\left( x \right) = x\sqrt {3{a^2} - 4{x^2}} \) trong khoảng \(\left( {0;\dfrac{{a\sqrt 3 }}{2}} \right)\)
\(f'\left( x \right) = \sqrt {3{a^2} - 4{x^2}} + x.\dfrac{{ - 4x}}{{\sqrt {3{a^2} - 4{x^2}} }} = \dfrac{{3{a^2} - 8{x^2}}}{{\sqrt {3{a^2} - 4{x^2}} }} = 0\) \( \Leftrightarrow x = \dfrac{{a\sqrt 6 }}{4}\).
Bảng biến thiên:
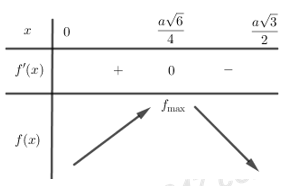
Từ bảng biến thiên ta thấy: Hàm số \(y = f\left( x \right)\) đạt GTLN tại \(x = \dfrac{{a\sqrt 6 }}{4}\) hay \({V_{S.ABC}}\) đạt GTLN tại \(x = \dfrac{{a\sqrt 6 }}{4}\).
Khi đó \({V_{\max }} = \dfrac{{a.\dfrac{{a\sqrt 6 }}{4}.\sqrt {3{a^2} - 4.\dfrac{{6{a^2}}}{{16}}} }}{6} = \dfrac{{{a^3}}}{8}\).
Chọn C.