Phương pháp giải:

Sử dụng MTCT tính \(y'\left( {{x}_{0}} \right)\) với \({{x}_{0}}\) là điểm bất kì thuộc các đáp án.

Lời giải chi tiết:

Sử dụng máy tính CASIO để thử từng đáp án. Để tìm hàm số nghịch biến trong (1;3) thì \(y'\le 0\,\,\,\forall x\in (1;3)\) nên ta thử với giá trị \(x=\dfrac{5}{2}\).

+) Đáp án A: \(y'=2{{x}^{2}}-8x+6\).

Nhập hàm y’ vào máy tính và tính với giá trị \(x=\dfrac{5}{2}\) ta được \(y'=-\dfrac{3}{2}<0\) nên hàm số nghịch biến trên (1;3).

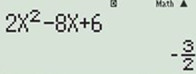
Đáp án A có thể đúng.

+) Đáp án B: \(y'=x-2\)

Nhập hàm tính giá trị của hàm y’ với giá trị \(x = \dfrac{3}{2}\) ta được \(y' = \dfrac{1}{2} > 0\) nên hàm số đồng biến.

Loại đáp án B.

+) Đáp án C: \(y'=\dfrac{{{x}^{2}}-2x}{{{\left( x-1 \right)}^{2}}}\)

Nhập hàm y’ vào máy tính và tính với giá trị \(x=\dfrac{5}{2}\) ta được \(y'=\dfrac{5}{9}>0\) nên hàm số đồng biến.

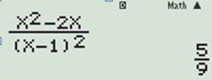 \(\Rightarrow \) Loại đáp án C.

+) Đáp án D: ĐK:

Ta có: \(y'=\dfrac{3}{{{\left( x-1 \right)}^{2}}}>0\,\,\forall x\ne 1\) nên hàm số luôn đồng biến trên \(\left( -\infty ;1 \right)\) và \(\left( 1;+\infty  \right)\).

Loại đáp án D.

Chọn A.