Câu hỏi
Hàm số \(y=\dfrac{m}{3}{{x}^{3}}-\left( m-1 \right){{x}^{2}}+3\left( m-2 \right)x+\dfrac{1}{3}\) đồng biến trên \(\left( {2; + \infty } \right)\) thì m thuộc tập nào:
- A \(m\in \left[ \dfrac{2}{3};+\infty \right)\)
- B \(m\in \left( -\infty ;\dfrac{-2-\sqrt{6}}{2} \right)\)
- C \(m\in \left( -\infty ;\dfrac{2}{3} \right)\)
- D \(m\in \left( -\infty ;-1 \right)\)
Phương pháp giải:
- Chọn m.
- Sử dụng MTCT tính \(y'\left( {{x}_{0}} \right)\) với \({{x}_{0}}\) là điểm bất kì thuộc các đáp án.
Lời giải chi tiết:
Ta có: \(y' = m{x^2} - 2\left( {m - 1} \right)x + 3\left( {m - 2} \right)\).
Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) khi \(y' \ge 0\) trong \(\left( 2;+\infty \right)\). Ta thử từng đáp án để chọn đáp án đúng.
+) Đáp án A: Với \(m = \dfrac{2}{3}\) ta có: \(y' = \dfrac{2}{3}{x^2} + \dfrac{2}{3}x - 4\)
Ta nhập hàm y’ vào máy tính và thử giá trị \(x = 2\) ta được \(y' = 0\) nên đáp án A có thể đúng.

Để chắc chắn, ta thử với giá trị \(x = 3\) ta được \(y' = 4 > 0\) nên hàm số đồng biến.
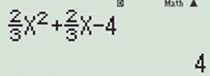
Vậy đáp án A đúng.
Chọn A.







