Câu hỏi
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \(\left( { - 1; + \infty } \right)\).
- A \(y = \dfrac{1}{3}{x^3} - {x^2} - 3x\)
- B \(y = \ln x\)
- C \(y={{e}^{{{x}^{2}}+2x}}\)
- D \(y=-{{x}^{4}}-\dfrac{4}{3}{{x}^{3}}\)
Phương pháp giải:
Sử dụng MTCT tính \(y'\left( {{x}_{0}} \right)\) với \({{x}_{0}}\) là điểm bất kì thuộc các đáp án.
Lời giải chi tiết:
Sử dụng máy tính CASIO dùng chức năng Shift \(\dfrac{d}{{dx}}{\left. {\left( {} \right)} \right|_{x = ?}}\) ta tính đạo hàm từng đáp án nếu đáp án nào ra kết quả 1 số \( \le 0\) thì đáp án đó đúng, còn đáp án nào ra kết quả > 0 thì đáp án đó sai.
Ta có:
+) Đáp án A. Tại \(x = 6\) ta có :
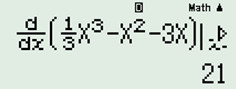\(>0\Rightarrow A\) sai.
+) Đáp án B: Ta sẽ thử với x = 1. Vì ĐKXĐ: \(x>0\).
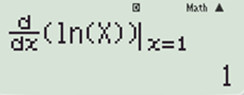\(\Rightarrow \) đáp án B \( y’ = 1 > 0 \Rightarrow B\) sai.
+) Đáp án C: Ta có: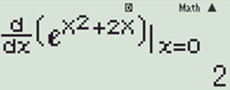 
\(\Rightarrow C\) sai.
Chọn D.
Câu hỏi trước
