Phương pháp giải:

- Đạo hàm hàm số \(f\left( x \right)\) đến cấp \(2019\) (tìm công thức tổng quát).

- Xét hàm \(y = {f^{\left( {2019} \right)}}\left( x \right)\) trên khoảng \(\left( {\frac{\pi }{{12}};\frac{{3\pi }}{8}} \right)\) và tìm điều kiện để bất phương trình \({f^{\left( {2019} \right)}}\left( x \right) > m\) nghiệm đúng với mọi \(x \in \left( {\frac{\pi }{{12}};\frac{{3\pi }}{8}} \right)\).

Lời giải chi tiết:

\(\begin{array}{l}f\left( x \right) = \cos 2x;\,\,f'\left( x \right) =  - 2\sin 2x;\,\,f''\left( x \right) =  - {2^2}\cos 2x;\,\,\,f'''\left( x \right) = {2^3}\sin 2x\\{f^{\left( 4 \right)}}\left( x \right) = {2^4}\cos 2x,{f^{\left( 5 \right)}}\left( x \right) =  - {2^5}\sin 2x,{f^{\left( 6 \right)}}\left( x \right) =  - {2^6}\cos 2x,{f^{\left( 7 \right)}}\left( x \right) = {2^7}\sin 2x\end{array}\)

Do đó:  \(\left\{ \begin{array}{l}{f^{\left( {4k} \right)}}\left( x \right) = {2^{4k}}\cos 2x\\{f^{\left( {4k + 1} \right)}}\left( x \right) =  - {2^{4k + 1}}\sin 2x\\{f^{\left( {4k + 2} \right)}}\left( x \right) =  - {2^{4k + 2}}\cos 2x\\{f^{\left( {4k + 3} \right)}}\left( x \right) = {2^{4k + 3}}\sin 2x\end{array} \right.\)

\( \Rightarrow {f^{\left( {2019} \right)}}\left( x \right) = {f^{\left( {4.504 + 3} \right)}}\left( x \right) = {2^{2019}}\sin 2x\).

Xét hàm \(y = {f^{\left( {2019} \right)}}\left( x \right) = {2^{2019}}\sin 2x\) trên  \(\left( {\frac{\pi }{{12}};\frac{{3\pi }}{8}} \right)\)  ta có:

+ Trên khoảng \(\left( {\frac{\pi }{{12}};\frac{\pi }{4}} \right)\) thì \(2x \in \left( {\frac{\pi }{6};\frac{\pi }{2}} \right) \Rightarrow \sin 2x \in \left( {\frac{1}{2};1} \right) \Rightarrow {2^{2019}}\sin 2x \in \left( {{2^{2018}};{2^{2019}}} \right)\) và hàm \(y = {2^{2019}}\sin 2x\) đồng biến trên khoảng này.

+ Trên khoảng \(\left( {\frac{\pi }{4};\frac{{3\pi }}{8}} \right)\) thì \(2x \in \left( {\frac{\pi }{2};\frac{{3\pi }}{4}} \right) \Rightarrow \sin 2x \in \left( {\frac{{\sqrt 2 }}{2};1} \right) \Rightarrow {2^{2019}}\sin 2x \in \left( {{2^{\frac{{4037}}{2}}};{2^{2019}}} \right)\)  và hàm \(y = {2^{2019}}\sin 2x\) nghịch biến trên khoảng này.

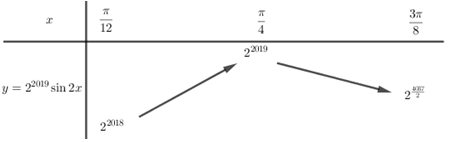
Bảng biến thiên:

Quan sát bảng biến thiên ta thấy, bất phương trình \({f^{\left( {2019} \right)}}\left( x \right) > m\) nghiệm đúng với mọi \(x \in \left( {\frac{\pi }{{12}};\frac{{3\pi }}{8}} \right)\) nếu \(m \le {2^{2018}}\).

Chọn B.