Câu hỏi
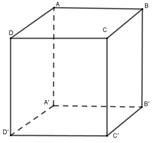
Cho khối hộp đứng có một mặt là hình vuông cạnh \(a\) và một mặt có diện tích là \(3{a^2}.\) Thể tích của khối hộp là
- A \({a^3}\)
- B \(3{a^3}\)
- C \(2{a^3}\)
- D \(4{a^3}\)
Phương pháp giải:
Thể tích khối hộp đứng có chiều cao \(h\) và diện tích đáy \(S\) là \(V = h.S\)
Lời giải chi tiết:
Giả sử \(ABB'A'\) là hình vuông cạnh \(a\) thì chiều cao hình hộp \(AA' = a\) và diện tích đáy hình hộp là \({S_{ABCD}} = 3{a^2}\)
Thể tích hình hộp là \(V = AA'.{S_{ABCD}} = a.3{a^2} = 3{a^3}.\)
Chọn B.
Câu hỏi trước
