Phương pháp giải:

Thể tích khối lăng trụ: \(V = Sh\).

Lời giải chi tiết:

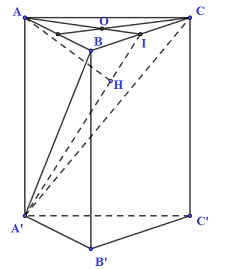
Gọi I là trung điểm cua BC, kẻ \(AH \bot A'I\).

\(\Delta ABC\) đều cạnh a  \( \Rightarrow AI = \dfrac{{a\sqrt 3 }}{2};\,\,{S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Ta có: \(\left\{ \begin{array}{l}AI \cap \left( {A'BC} \right) = \left\{ I \right\}\\AI = 3.OI\end{array} \right. \Rightarrow d\left( {O;\left( {A'BC} \right)} \right) = \dfrac{1}{3}d\left( {A;\left( {A'BC} \right)} \right)\)

Ta có: \(\left\{ \begin{array}{l}BC \bot AI\\BC \bot AA'\end{array} \right. \Rightarrow BC \bot \left( {AA'I} \right) \Rightarrow BC \bot AH\)

Mà \(AH \bot A'I \Rightarrow AH \bot \left( {A'BC} \right) \Rightarrow d\left( {A;\left( {A'BC} \right)} \right) = AH\)

\( \Rightarrow d\left( {O;\left( {A'BC} \right)} \right) = \dfrac{1}{3}AH = \dfrac{a}{6} \Rightarrow AH = \dfrac{a}{2}\)

\(\Delta AA'I\) vuông tại A, \(AH \bot A'I\)

\( \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{I^2}}} + \dfrac{1}{{AA{'^2}}} \Leftrightarrow \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} = \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}} + \dfrac{1}{{AA{'^2}}}\)

\( \Leftrightarrow \dfrac{4}{{{a^2}}} = \dfrac{4}{{3{a^2}}} + \dfrac{1}{{AA{'^2}}}\)\( \Leftrightarrow AA' = \dfrac{{a\sqrt 6 }}{4}\)

Thể tích khối lăng trụ ABC.A’B’C’ là: \(V = {S_{ABC}}.AA' = \dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{{a\sqrt 6 }}{4} = \dfrac{{3{a^3}\sqrt 2 }}{{16}}\).

Chọn: A