Phương pháp giải:

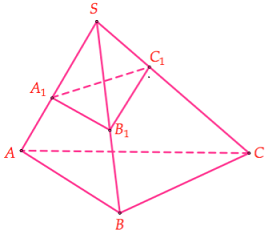
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác

(Công thức Simson): Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó,

\(\dfrac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \dfrac{{S{A_1}}}{{SA}}.\dfrac{{S{B_1}}}{{SB}}.\dfrac{{S{C_1}}}{{SC}}\)

Lời giải chi tiết:

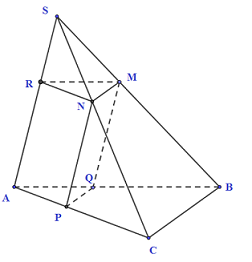
Dựng MN//BC \(\left( {N \in SC} \right)\), MQ//SA  \(\left( {Q \in AB} \right)\), PQ//BC

\(\left( {P \in AC} \right) \Rightarrow MNPQ\) là thiết diện cần dựng.

\({V_1}\) là thể tích khối đa giác SNM.APQ. Dựng MR // AB \(\left( {R \in SA} \right)\). Khi đó, khối đa giác SNM.APQ được chia làm 2 phần: khối chóp tam giác S.RMN và khối lăng trụ RMN.AQP.

Giả sử \(\dfrac{{SM}}{{SB}} = x\).

Ta có: \(\dfrac{{{V_{S.RMN}}}}{{{V_{S.ABC}}}} = {\left( {\dfrac{{SM}}{{SB}}} \right)^3} = {x^3} \Rightarrow {V_{S.RMN}} = {x^3}.{V_{S.ABC}}\)

\({V_{RMN.ABC}} = d\left( {M;\left( {ABC} \right)} \right).{S_{APQ}} = \left( {1 - x} \right)d\left( {S;\left( {ABC} \right)} \right).{S_{ABC}} = 3\left( {1 - x} \right).{x^2}.{V_{S.ABC}}\)\( \Rightarrow {V_1} = 3\left( {1 - x} \right).{x^2}.V\)

Mà \(\dfrac{{{V_1}}}{V} = \dfrac{{20}}{{27}} \Rightarrow {x^3} + 3\left( {1 - x} \right).{x^2} = \dfrac{{20}}{{27}} \Leftrightarrow  - 2{x^3} + 3x - \dfrac{{20}}{{27}} = 0 \Leftrightarrow x = \dfrac{2}{3}\).

Vậy \(\dfrac{{SM}}{{SB}} = \dfrac{2}{3}\).

Chọn: A