Cách tính mức cường độ âm ứng dụng logarit - Toán 11

Tai người nhạy cảm với nhiều cường độ âm thanh khác nhau. Chúng ta lấy cường độ tham chiếu \({I_0} = {10^{ - 12}}{\rm{W/}}{{\rm{m}}^2}\) (oát trên mét vuông) ở tần số 1 000 hertz, nó đo âm thanh nhỏ nhất mà tai người có thể phát hiện được (gọi là ngưỡng nghe). Cảm giác tâm lí về âm lượng thay đổi theo lộgarit của cường độ (định luật Weber-Fechner), do đó mức cường độ âm \(L\), đo bằng deciben (dB), được định nghĩa là \(L = 10\log \frac{I}{{{I_0}}}\).

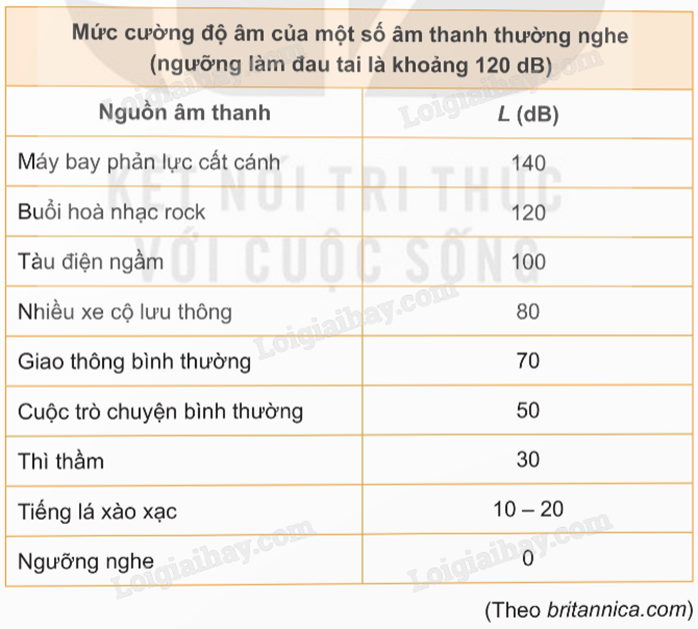
Mức cường độ âm đặc trưng cho độ to nhỏ của âm. Công thức trên cho thấy: Khi cường độ của âm tăng lên \({10^2},{10^3},...\) lần thì cảm giác về độ to nhỏ của âm tăng lên gấp 2, 3, ... lần.

Áp dụng công thức \(L = 10\log \frac{I}{{{I_0}}}\), với \({I_0} = {10^{ - 12}}{\rm{W/}}{{\rm{m}}^2}\).

Ví dụ minh hoạ:

Cường độ của âm thanh giao thông tại một ngã tư đông đúc đo được là \(2,{0.10^{ - 5}}{\rm{W}}/{m^2}\). Tính mức cường độ âm tính bằng decibel.

Giải:

Mức cường độ âm tính bằng decibel là:

\(L = 10\log \frac{{2,{{0.10}^{ - 5}}}}{{{{10}^{ - 12}}}} = 73,01029996\) (dB).