Cách tính độ dài đoạn thẳng bằng cách sử dụng định lí Thalès - Toán 8

Để tính độ dài đoạn thẳng bằng cách sử dụng định lí Thalès chúng ta cần thực hiện các bước như sau:

Bước 1: Xác định đường thẳng song song với một cạnh của tam giác liên quan đến các đoạn thẳng cần tính.

Bước 2: Áp dụng định lí Thalès để lập hệ thức của các đoạn thẳng tỉ lệ.

Bước 3: Thay số vào hệ thức và áp dụng tính chất của tỉ lệ thức để tìm độ dài đoạn thẳng.

Bước 4: Kết luận.

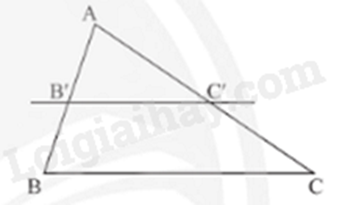
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.

Ví dụ: Xét \(\Delta ABC\) có d // BC và cắt AB tại M, cắt AC tại N. Theo định lí Thalès, ta có các tỉ lệ sau:

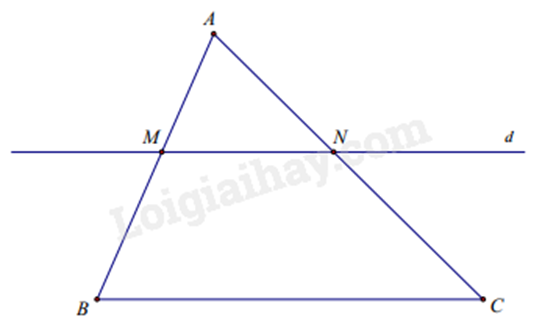
(1) \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); (2) \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\); (3) \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).

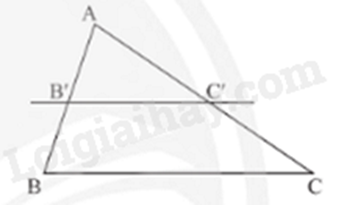
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

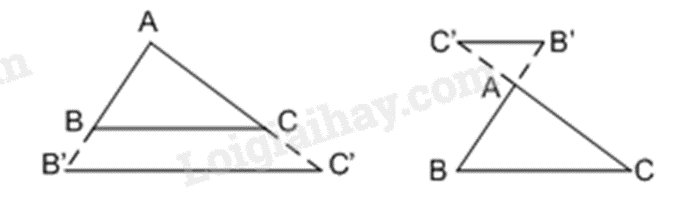
Ở hai hình trên, tam giác ABC có BC // B’C’ suy ra \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).

Ví dụ:

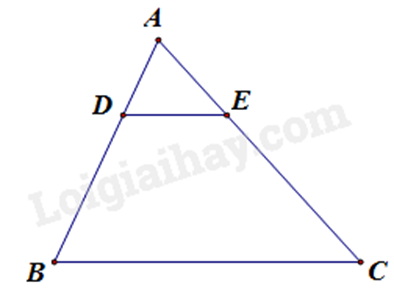
Cho tam giác ABC có DE // BC thì \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).

Giả sử tất cả các biểu thức đều có nghĩa, nếu \(\frac{a}{b} = \frac{c}{d}\) thì:

+) ad = bc.

+) \(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}}\).

+) \(\frac{{a + b}}{b} = \frac{{c + d}}{d}\); \(\frac{{a - b}}{d} = \frac{{c - d}}{d}\).

+) \(\frac{a}{c} = \frac{b}{d}\).