Copyright © 2021 loigiaihay.com
Từ điển môn Toán lớp 8 - Tổng hợp các khái niệm Toán 8
Định lí Thalès trong tam giác - Từ điển môn Toán 8
Định lí Thalès trong tam giác - Từ điển môn Toán 8 Cách chứng minh các hệ thức hình học bằng định lí Thalès - Toán 8
1. Cách chứng minh các hệ thức hình học bằng định lí Thalès
Để chứng minh các hệ thức hình học bằng định lí Thalès, ta sử dụng các kiến thức:
+ Định lí Thalès
+ Sử dụng tính chất tỉ lệ thức.
2. Định lí Thalès
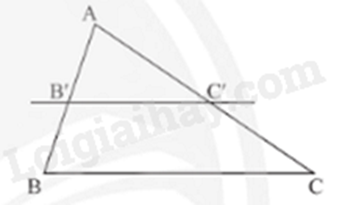
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.
|
GT |
\(\Delta ABC,B'C'//BC(B' \in AB,C' \in AC)\) |
|
KL |
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}};\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}};\frac{{B'B}}{{AB}} = \frac{{C'C}}{{AC}}\) |
Ví dụ: Xét \(\Delta ABC\) có d // BC và cắt AB tại M, cắt AC tại N. Theo định lí Thalès, ta có các tỉ lệ sau:
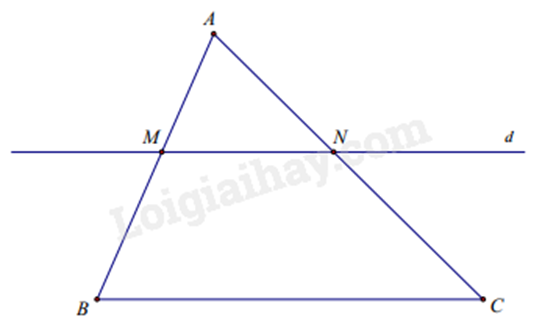
(1) \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); (2) \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\); (3) \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
3. Tỉ lệ thức
Giả sử tất cả các biểu thức đều có nghĩa, nếu \(\frac{a}{b} = \frac{c}{d}\) thì:
+) ad = bc.
+) \(\frac{a}{b} = \frac{c}{d} = \frac{{a + c}}{{b + d}} = \frac{{a - c}}{{b - d}}\).
+) \(\frac{{a + b}}{b} = \frac{{c + d}}{d}\); \(\frac{{a - b}}{d} = \frac{{c - d}}{d}\).
+) \(\frac{a}{c} = \frac{b}{d}\).
