Cách tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn - Toán 9

+) Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.

+) Tỉ số giữa cạnh kề và cạnh huyền được gọi là cos (cosin) của góc α, kí hiệu là cos α.

+) Tỉ số giữa cạnh đối và cạnh kề được gọi là tan (tang) của góc α, kí hiệu là tan α.

+) Tỉ số giữa cạnh kề và cạnh đối được gọi là cot (côtang) của góc α, kí hiệu là cot α.

\(\sin \alpha = \frac{\text{cạnh đối}}{\text{cạnh huyền}}\);\(\cos \alpha = \frac{\text{cạnh kề}}{\text{cạnh huyền}}\);

\(\tan \alpha = \frac{\text{cạnh đối}}{\text{cạnh kề}}\);\(\cot \alpha = \frac{\text{cạnh kề}}{\text{cạnh đối}}\).

Quy ước:

\(\begin{array}{l}{\sin ^2}\alpha  = {\left( {\sin \alpha } \right)^2};\\{\cos ^2}\alpha  = {\left( {\cos \alpha } \right)^2};\\{\tan ^2}\alpha  = {\left( {\tan \alpha } \right)^2};\\{\cot ^2}\alpha  = {\left( {\cot \alpha } \right)^2}.\end{array}\)

Tip học thuộc nhanh:

Sin đi học

Cos không hư

Tang đoàn kết

Cotang kết đoàn

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

Cạnh góc vuông = (cạnh huyền ) × (sin góc đối)

= (cạnh huyền ) × (cosin góc kề)

Ví dụ:

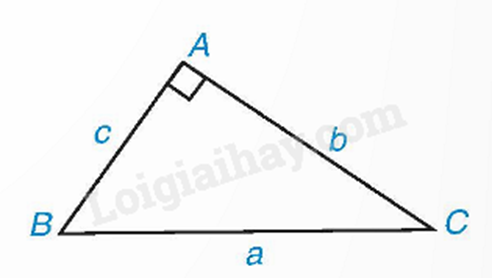
Trong tam giác ABC vuông tại A, ta có:

\(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\)