Giải tam giác vuông là gì? Cách tính cạnh, góc và diện tích tam giác - Toán 9

Giải một tam giác vuông là tìm ra các yếu tố còn lại của tam giác khi đã biết trước hai yếu tố. Trong quá trình giải, phải có ít nhất một yếu tố về độ dài cạnh, và không cần biết đến góc vuông của tam giác. Các phương pháp giải tam giác vuông có thể sử dụng định lý Pythagore, các tỉ lệ cơ bản của tam giác vuông, hay các công thức khác để tìm ra các yếu tố còn lại, bao gồm cạnh, đường cao, chu vi và diện tích của tam giác.

Để tính được cạnh, góc, diện tích tam giác, ta cần vận dụng các kiến thức cơ bản sau:

1. Tỉ số lượng giác của góc nhọn

+ \(\sin \alpha = \frac{\text{cạnh đối}}{\text{cạnh huyền}}\);\(\cos \alpha = \frac{\text{cạnh kề}}{\text{cạnh huyền}}\);

+ \(\tan \alpha = \frac{\text{cạnh đối}}{\text{cạnh kề}}\);\(\cot \alpha = \frac{\text{cạnh kề}}{\text{cạnh đối}}\).

+ Với \({0^0} < \alpha  < {90^0}\), ta có:

\(\sin \left( {{{90}^0} - \alpha } \right) = \cos \alpha \); \(\cos \left( {{{90}^0} - \alpha } \right) = \sin \alpha \);

\(\tan \left( {{{90}^0} - \alpha } \right) = \cot \alpha \); \(\cot \left( {{{90}^0} - \alpha } \right) = \tan \alpha \).

2. Hệ thức giữa cạnh và góc trong tam giác

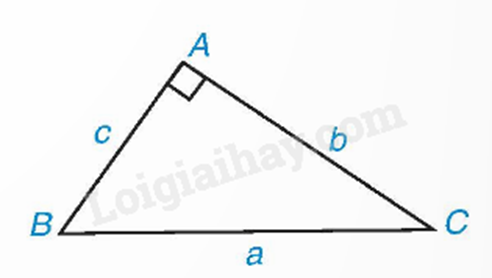
Trong tam giác ABC vuông tại A, ta có:

\(b = a.\sin B = a.\cos C;c = a.\sin C = a.\cos B.\)

\(b = c.\tan B = c.\cot C;c = b.\tan C = b.\cot B.\)

3. Công thức lượng giác liên quan

+) Với góc nhọn \(\alpha \), ta có:

\(0 < \sin \alpha  < 1\); \(0 < \cos \alpha  < 1\); \(\tan \alpha  > 0\); \(\cot \alpha  > 0\); \(\cot \alpha  = \frac{1}{{\tan \alpha }}\).

+) \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

+) \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\)

+) \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\)

+) \(\tan \alpha .\cot \alpha  = 1\)

+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha  + 1\)

+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha  + 1\)

4. Định lí Pythagore

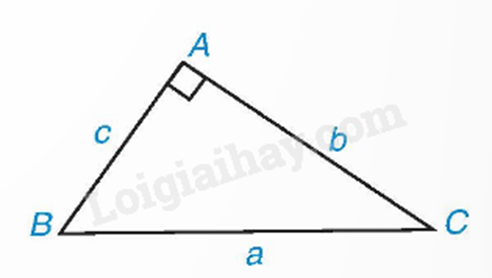
Trong tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\).