Cách ứng dụng lượng giác để ước lượng chiều cao - Toán 9

Lượng giác được sử dụng để đo chiều cao của các toà nhà, núi, cây, v.v. Chiều cao của một toà nhà hoặc một ngọn núi có thể dễ dàng được xác định bằng cách đo khoảng cách theo chiều ngang từ chân núi và góc nâng lên đỉnh núi.

Chúng ta hãy lấy một ví dụ để hiểu khái niệm này:

Một cậu bé đang đứng gần một toà nhà và tự hỏi: "Chiều cao của toà nhà là bao nhiêu?"

Sử dụng các công thức lượng giác, chiều cao có thể được tính toán nếu khoảng cách giữa toà nhà và cậu bé và góc tạo thành khi nhìn toà nhà từ mặt đất được cung cấp.

Giả sử góc tạo thành là \(\alpha \).

\(\tan \alpha \) = chiều cao / khoảng cách giữa cậu bé và toà nhà.

Khoảng cách = chiều cao / \(\tan \alpha \)

Giả sử khoảng cách là 30m và góc tạo thành là \(45^\circ \) thì:

Chiều cao = \(\frac{{30}}{{\tan 45^\circ }}\)

Vì \(\tan 45^\circ  = 1\) nên chiều cao bằng 30m.

Phương pháp giải:

- Sử dụng tỉ số lượng giác của góc nhọn, hệ thức lượng giữa cạnh và góc trong tam giác để tính toán, ước lượng chiều cao.

- Xác định các yếu tố đã cho của đề bài để lựa chọn tỉ số lượng giác, hệ thức phù hợp với bài toán.

+) Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.

+) Tỉ số giữa cạnh kề và cạnh huyền được gọi là cos (cosin) của góc α, kí hiệu là cos α.

+) Tỉ số giữa cạnh đối và cạnh kề được gọi là tan (tang) của góc α, kí hiệu là tan α.

+) Tỉ số giữa cạnh kề và cạnh đối được gọi là cot (côtang) của góc α, kí hiệu là cot α.

\(\sin \alpha = \frac{\text{cạnh đối}}{\text{cạnh huyền}}\);\(\cos \alpha = \frac{\text{cạnh kề}}{\text{cạnh huyền}}\);

\(\tan \alpha = \frac{\text{cạnh đối}}{\text{cạnh kề}}\);\(\cot \alpha = \frac{\text{cạnh kề}}{\text{cạnh đối}}\).

Quy ước:

\(\begin{array}{l}{\sin ^2}\alpha  = {\left( {\sin \alpha } \right)^2};\\{\cos ^2}\alpha  = {\left( {\cos \alpha } \right)^2};\\{\tan ^2}\alpha  = {\left( {\tan \alpha } \right)^2};\\{\cot ^2}\alpha  = {\left( {\cot \alpha } \right)^2}.\end{array}\)

Tip học thuộc nhanh:

Sin đi học

Cos không hư

Tang đoàn kết

Cotang kết đoàn

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

Cạnh góc vuông = (cạnh huyền ) × (sin góc đối)

= (cạnh huyền ) × (cosin góc kề)

Ví dụ:

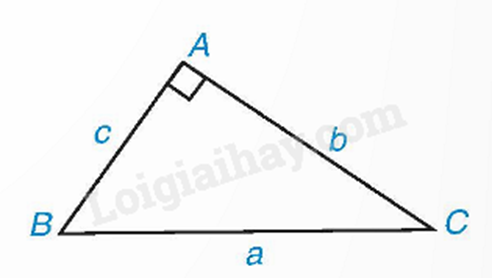
Trong tam giác ABC vuông tại A, ta có:

\(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\)

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề.

Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối) 

= (cạnh góc vuông còn lại ) × (cot góc kề)

Ví dụ:

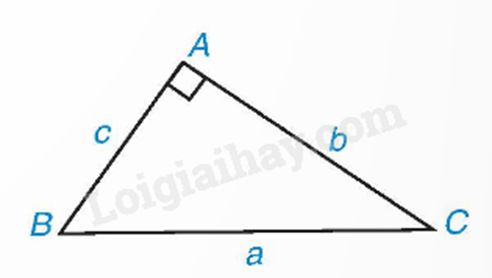
Trong tam giác ABC vuông tại A, ta có:

\(\begin{array}{l}b = c.\tan B = c.\cot C;\\c = b.\tan C = b.\cot B.\end{array}\)