Copyright © 2021 loigiaihay.com
Từ điển Toán 9 | Các dạng bài tập Toán 9
Hình nón - Từ điển môn Toán 9
Hình nón - Từ điển môn Toán 9 Cách tạo lập hình nón - Toán 9
1. Định nghĩa Hình nón
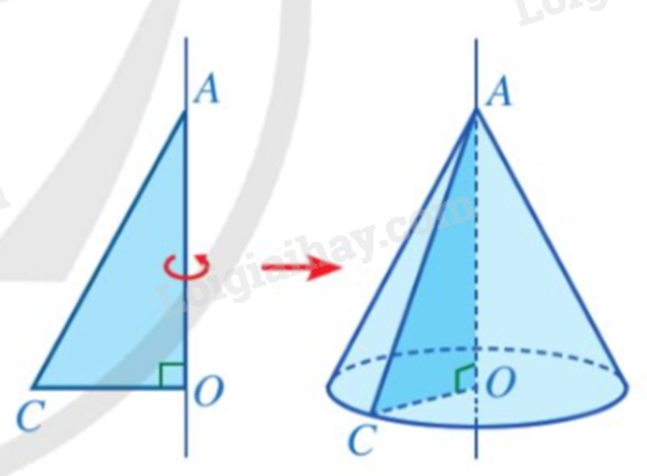
Hình nón là hình được tạo ra khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác đó.
2. Công thức tính độ dài đường sinh
Nếu gọi độ dài đường sinh, chiều cao và bán kính đáy của hình nón lần lượt là \(l,h,r\) thì theo định lí Pythagore ta có:
\({l^2} = {r^2} + {h^2}\).
3. Cách tạo lập hình nón
Để tạo hình nón có chiều cao h và bán kính đáy r ta làm ba bước như sau:
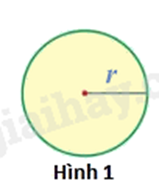
Bước 1: Cắt miếng bìa có dạng hình tròn với bán kính r (hình 1).
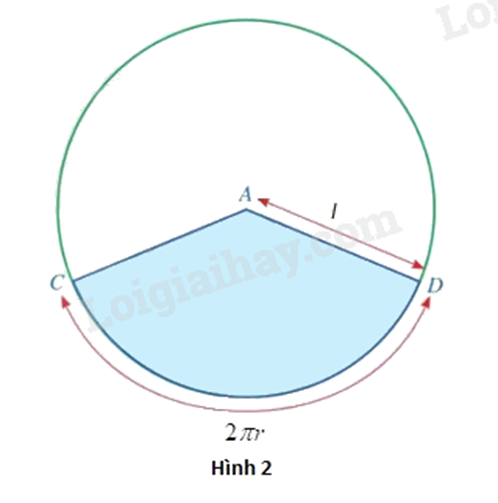
Bước 2: Cắt một tấm bìa hình quạt tròn có bán kính bằng độ dài đường sinh \({l^2} = {r^2} + {h^2}\) và độ dài
cung của hình quạt tròn bằng \(2\pi r\) (hình 2).
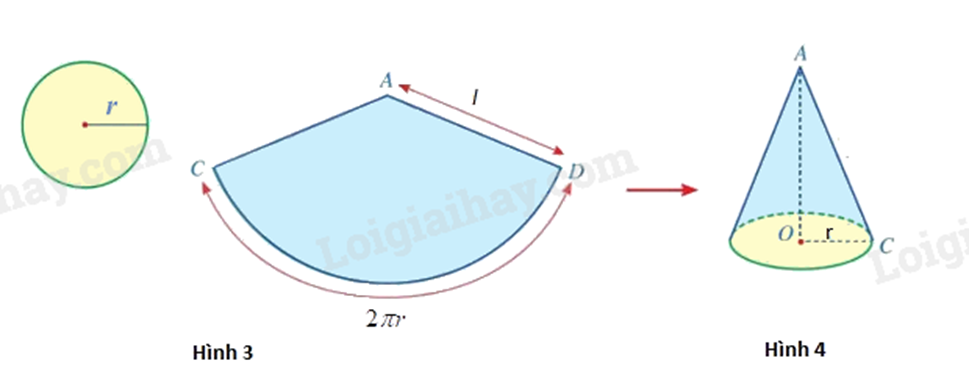
Bước 3: Ghép và dán các miếng bìa vừa cắt ở bước 1, bước 2 (hình 3), ta được một hình nón (hình 4).
