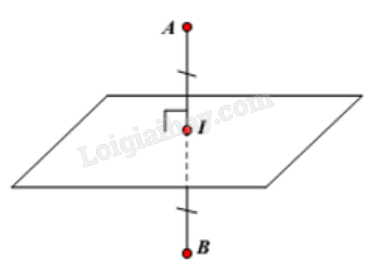
Cách lập phương trình mặt phẳng trung trực của đoạn thẳng - Toán 12

Mặt phẳng trung trực của đoạn thẳng là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.

Mặt phẳng trung trực của đoạn thẳng là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.

Trong hệ toạ độ Oxyz, cho đoạn thẳng AB. Để lập phương trình mặt phẳng trung trực của AB, ta thực hiện:

Bước 1: Tìm trung điểm của AB.

Giả sử I là trung điểm của AB, ta có toạ độ của I là: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2}\\{z_I} = \frac{{{z_A} + {z_B}}}{2}\end{array} \right.\)

Bước 2: Tính toạ độ \(\overrightarrow {AB} \).

\(\overrightarrow {AB}  = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).

Bước 3: Lập phương trình mặt phẳng trung trực của AB.

Gọi mặt phẳng đó là \(\left( \alpha  \right)\).

\(\left( \alpha  \right)\) đi qua \(I\left( {{x_I};{y_I};{z_I}} \right)\) và nhận \(\overrightarrow {AB}  = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\) làm vecto pháp tuyến. Do đó, phương trình của \(\left( \alpha  \right)\) là:

\(\left( {{x_B} - {x_A}} \right)\left( {x - {x_I}} \right) + \left( {{y_B} - {y_A}} \right)\left( {y - {y_I}} \right) + \left( {{z_B} - {z_A}} \right)\left( {z - {z_I}} \right) = 0\).

Ví dụ minh hoạ:

Trong không gian Oxyz, tìm phương trình mặt phẳng trung trực của đoạn thẳng AB, biết A(2;1;4), B(-1;-3;-5).

Giải:

Gọi I là trung điểm của AB, ta có \(I = \left( {\frac{{2 - 1}}{2};\frac{{1 - 3}}{2};\frac{{4 - 5}}{2}} \right) = \left( {\frac{1}{2}; - 1; - \frac{1}{2}} \right)\).

Gọi (P) là mặt phẳng cần tìm. Khi đó (P) đi qua I và có vecto pháp tuyến là \(\overrightarrow {BA} = (3;4;9)\).

Phương trình mặt phẳng (P) là

\(3\left( {x - \frac{1}{2}} \right) + 4(y + 1) + 9\left( {z + \frac{1}{2}} \right) = 0 \Leftrightarrow 3x + 4y + 9z + 7 = 0\).