Cách làm bài tập phản ứng tráng bạc, lên men glucose - Hoá 12

1. Cu(OH)₂/OH^-(t^o) tạo kết tủa đỏ gạch Cu₂O

CH­­₂OH-[CHOH]₄-CHO + 2Cu(OH)₂ +NaOH   CH­­₂OH-[CHOH]₄-COONa + Cu₂O +3H₂O

                                                                         Sodium gluconate

2. Thuốc thử Tollens

CH­­₂OH-[CHOH]₄-CHO + 2[Ag(NH₃)₂]OH →  CH­­₂OH-[CHOH]₄-COONH₄ + 2Ag + 3NH₃+H₂O

C₆H₁₂O₆ 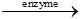  2 C­_2­H₅OH  + 2 CO₂     

C₆H₁₂O₆ 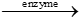 2 CH₃CH(OH)COOH

- Phản ứng tráng gương của glucose: 1C₆H₁₂O₆ → 2Ag

- Phản ứng lên men của glucose: C₆H₁₂O₆ → 2C₂H₅OH + 2CO₂

Bài toán có hiệu suất:

- Tính toán bình thường, đến kết quả cuối cùng ta xem chất đang tính nếu:

+ Trước mũi tên (→)  chất tham gia phản ứng thì lấy: Kết quả. \(\frac{{100}}{{\rm{H}}}\).

+ Sau mũi tên (→)  chất tạo thành thì lấy: Kết quả. \(\frac{{\rm{H}}}{{{\rm{100}}}}\).

- Bài toán cho hao hụt a% thì xem hiệu suất là :(100 – a)%.

- Nếu bài toán có nhiều hiệu suất : 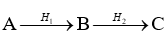 (H₁, H₂ là hiệu suất phản ứng)

                     m_A = KQ. \(\frac{{{\rm{100}}}}{{{{\rm{H}}_{\rm{1}}}}}.\frac{{{\rm{100}}}}{{{{\rm{H}}_2}}}\)   ;               m_C = KQ. \(\frac{{{{\rm{H}}_{\rm{1}}}}}{{{\rm{100}}}}.\frac{{{{\rm{H}}_2}}}{{{\rm{100}}}}\)  

- Trong bài toán có hiệu suất nhưng các chất cùng một bên thì không tính hiệu suất.

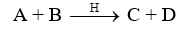
+Từ dữ liệu chất A tính ra chất B hoặc từ chất C mà tính ra chất D thì không xử lý hiệu suất.

+ Từ dữ liệu chất A, B tính ra C, D hoặc ngược lại thì ta phải xử lý hiệu suất

Bài toán tính hiệu suất:

         \(H = \frac{{LTTp/u}}{{LLTb/d}}.100\% \)

Bài toán độ alcohol: Tương quan giữa khối lượng và thể tích: gam ---- mL ; kg---- lít

                                    Độ cồn\({\rm{ = }}\frac{{{{\rm{V}}_{\rm{R}}}}}{{{{\rm{V}}_{{\rm{ddR}}}}}}{\rm{.10}}{{\rm{0}}^{\rm{0}}}\)  ; \({{\rm{m}}_{\rm{R}}}{\rm{ =  }}{{\rm{V}}_{\rm{R}}}{\rm{.}}{{\rm{D}}_{\rm{R}}}\)